【题目】如图,在四棱锥![]() 中,底面为直角梯形,
中,底面为直角梯形, ![]() ,
, ![]() ,
, ![]() 垂直于底面
垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
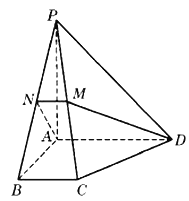
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求四棱锥的体积![]() 和截面
和截面![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据线面垂直性质定理得![]() ,而
,而![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() , 再由等腰三角形性质得
, 再由等腰三角形性质得![]() ,因此由线面垂直判定定理得
,因此由线面垂直判定定理得![]() 平面
平面![]() ,即证得
,即证得![]() ;(2)易得四棱锥
;(2)易得四棱锥![]() 的高
的高![]() ,再根据锥体体积公式得四棱锥的体积
,再根据锥体体积公式得四棱锥的体积![]() ;要求截面
;要求截面![]() 的面积,先确定截面
的面积,先确定截面![]() 的形状:由三角形中位线性质得
的形状:由三角形中位线性质得![]() ,即得
,即得![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,即四边形
,即四边形![]() 是直角梯形,最后利用直角梯形面积公式求解面积.
是直角梯形,最后利用直角梯形面积公式求解面积.
试题解析:(Ⅰ)证明:∵![]() 是
是![]() 的中点,
的中点, ![]() ,∴
,∴![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]()
∴![]() .
.
(Ⅱ)解:由![]() ,得底面直角梯形
,得底面直角梯形![]() 的面积
的面积![]() ,
,
由![]() 底面
底面![]() ,得四棱锥
,得四棱锥![]() 的高
的高![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
由![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,得
的中点,得![]() ,且
,且![]() ,
,
又![]() ,故
,故![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故![]() ,∴四边形
,∴四边形![]() 是直角梯形,
是直角梯形,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴截面![]() 的面积
的面积![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将圆
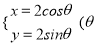 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的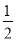 倍,得到曲线
倍,得到曲线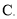
(1)求出
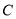 的普通方程;
的普通方程;(2)设直线
 :
: 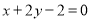 与
与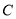 的交点为
的交点为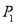 ,
, 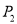 ,以坐标原点为极点,
,以坐标原点为极点, 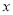 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段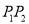 的中点且与
的中点且与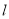 垂直的直线的极坐标方程.
垂直的直线的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=2ax2﹣2bx﹣a+b(a,b∈R,a>0),g(x)=2ax﹣2b
(1)若 时,求f(sinθ)的最大值;
时,求f(sinθ)的最大值;
(2)设a>0时,若对任意θ∈R,都有|f(sinθ)|≤1恒成立,且g(sinθ)的最大值为2,求f(x)的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若 , 试求f(x)在区间[﹣2,6]上的最值;
, 试求f(x)在区间[﹣2,6]上的最值; -
科目: 来源: 题型:
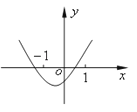
查看答案和解析>>【题目】已知函数f(x)=(x﹣a)(x﹣b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为( )
A.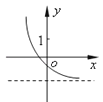
B.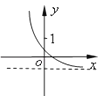
C.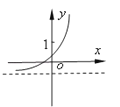
D.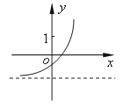
-
科目: 来源: 题型:
查看答案和解析>>【题目】用二分法研究函数f(x)=x3+3x﹣1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈ ,第二次应计算的f(x)的值为f( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ln(3+x)+ln(3﹣x).
(Ⅰ)求函数y=f(x)的定义域;
(Ⅱ)判断函数y=f(x)的奇偶性;
(Ⅲ)若f(2m﹣1)<f(m),求m的取值范围.
相关试题

