【题目】已知直线l: 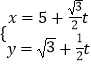 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为ρ=2cosθ.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为(5, ![]() ),直线l与曲线C的交点为A,B,求|MA||MB|的值.
),直线l与曲线C的交点为A,B,求|MA||MB|的值.
参考答案:
【答案】
(1)解:∵ρ=2cosθ,∴ρ2=2ρcosθ,∴x2+y2=2x,故它的直角坐标方程为(x﹣1)2+y2=1
(2)解:直线l: 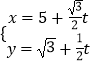 (t为参数),普通方程为
(t为参数),普通方程为 ![]() ,(5,
,(5, ![]() )在直线l上,
)在直线l上,
过点M作圆的切线,切点为T,则|MT|2=(5﹣1)2+3﹣1=18,
由切割线定理,可得|MT|2=|MA||MB|=18
【解析】(1)曲线的极坐标方程即ρ2=2ρcosθ,根据极坐标和直角坐标的互化公式得x2+y2=2x,即得它的直角坐标方程;(2)直线l的方程化为普通方程,利用切割线定理可得结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a∈R,函数f(x)=x|x﹣a|+2x.
(1)若a=2,求函数f(x)在区间[0,3]上的最大值;
(2)若a>2,写出函数f(x)的单调区间(不必证明);
(3)若存在a∈[﹣2,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数解,求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
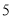 ,矩形
,矩形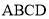 中,
中, 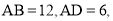 ,
, 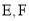 分别为
分别为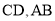 边上的点,且
边上的点,且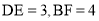 ,将
,将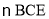 沿
沿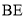 折起至
折起至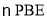 位置(如图
位置(如图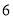 所示),连结
所示),连结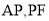 ,其中
,其中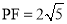 .
.(Ⅰ) 求证:
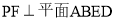 ;
; (Ⅱ) 在线段
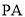 上是否存在点
上是否存在点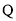 使得
使得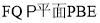 ?若存在,求出点
?若存在,求出点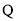 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.(Ⅲ) 求点
 到
到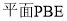 的距离.
的距离.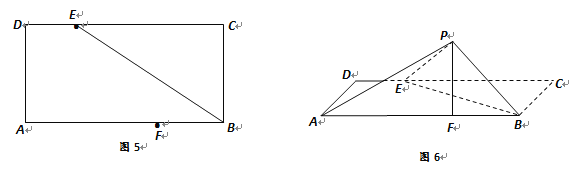
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合 A={x|2<x<4},B={a<x<3a}.
(1)若A∩B≠,求实数a的范围.
(2)若A∪B={x|2<x<6},求实数a的值. -
科目: 来源: 题型:
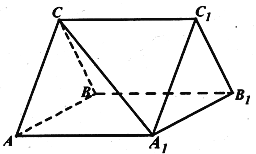
查看答案和解析>>【题目】(本小题满分13分)如图,三棱柱
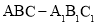 中,
中,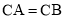 ,
,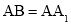 ,
, .
.
(1)证明:
 ;
;(2)若
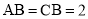 ,
,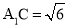 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,将曲线
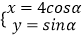 (α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度.
(α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=
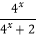 ,x∈R.
,x∈R.
(1)求证:对一切实数x,f(x)=f(1﹣x)恒为定值.
(2)计算:f(﹣6)+f(﹣5)+f(﹣4)+f(﹣3)+…+f(0)+…+f(6)+f(7).
相关试题

