【题目】已知椭圆![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,三角形
两点,三角形![]() 的周长为
的周长为![]() .
.
(1)求椭圆的方程;
(2)若弦![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用椭圆的离心率以及![]() 的周长为8,求出a,c,b,即可得到椭圆的方程,
的周长为8,求出a,c,b,即可得到椭圆的方程,
(2)求出直线方程与椭圆方程联立,点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() 求出A,B坐标,然后求解三角形的面积即可.
求出A,B坐标,然后求解三角形的面积即可.
试题解析:
(1)三角形![]() 的周长
的周长![]() ,所以
,所以![]() .
.
离心率![]() ,所以
,所以![]() ,则
,则![]() .
.
椭圆的方程为: ![]()
(2)设点![]() 的坐标为
的坐标为![]() ,
, ![]() 的坐标为
的坐标为![]() ,
, ![]() 的斜率为
的斜率为![]() (
(![]() 显然存在)
显然存在)

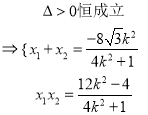
![]() .
.
![]() .
.
点睛: 本题主要考查直线与圆锥曲线位置关系,所使用方法为韦达定理法:因直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用韦达定理直接解决,但应注意不要忽视判别式的作用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数f(x)=4sin(2x+
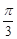 ), (x∈R)有下列命题:
), (x∈R)有下列命题:①y=f(x)是以2π为最小正周期的周期函数;
② y=f(x)可改写为y=4cos(2x-
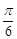 );
);③y=f(x)的图象关于(-
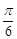 ,0)对称;
,0)对称;④ y=f(x)的图象关于直线x=-
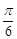 对称;
对称;其中正确的序号为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列
 中,
中, ,前
,前 项和
项和 满足条件
满足条件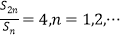 ,
,(1)求数列
 的通项公式和
的通项公式和 ;
;(2)记
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,长方形材料
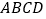 中,已知
中,已知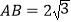 ,
,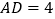 .点
.点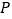 为材料
为材料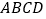 内部一点,
内部一点, 于
于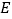 ,
,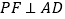 于
于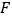 ,且
,且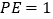 ,
,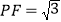 . 现要在长方形材料
. 现要在长方形材料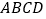 中裁剪出四边形材料
中裁剪出四边形材料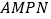 ,满足
,满足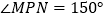 ,点
,点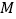 、
、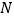 分别在边
分别在边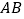 ,
,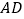 上.
上.(1)设
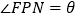 ,试将四边形材料
,试将四边形材料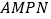 的面积表示为
的面积表示为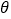 的函数,并指明
的函数,并指明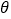 的取值范围;
的取值范围;(2)试确定点
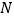 在
在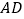 上的位置,使得四边形材料
上的位置,使得四边形材料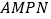 的面积
的面积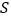 最小,并求出其最小值.
最小,并求出其最小值.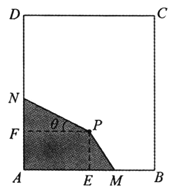
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量
 =[
=[  ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
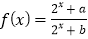 .
.(1)当
 ,
, 时,求满足
时,求满足 的
的 的值;
的值;(2)若函数
 是定义在
是定义在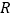 上的奇函数.
上的奇函数. ①存在
 ,使得不等式
,使得不等式 有解,求实数
有解,求实数 的取值范围;
的取值范围;②若函数
 满足
满足 ,若对任意
,若对任意 且
且 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 的前
的前 项和为
项和为 ,
, ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)设数列
 满足:
满足:对于任意
 ,都有
,都有 成立.
成立.①求数列
 的通项公式;
的通项公式;②设数列
 ,问:数列
,问:数列 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
相关试题

