【题目】某学习兴趣小组开展“学生语文成绩与外语成绩的关系”的课题研究,考察该校高二年级800名学生上学期期末的语文和外语成绩,按是否优秀分类得结果:语文和外语成绩都优秀的有60人,语文成绩优秀但外语成绩不优秀的有140人,外语成绩优秀但语文成绩不优秀的有100人.
(Ⅰ)能否有![]() 的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记所抽取的成绩中,语文、外语两科成绩至少有一科优秀的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
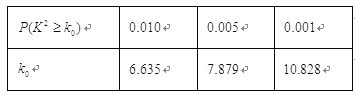
附:![]() .
.
参考答案:
【答案】(1) 有![]() 的把握(2)见解析
的把握(2)见解析
【解析】试题分析:(1)根据卡方公式计算![]() ,再与参考数据比较得是否有把握(2)有放回事件,可看作为独立重复试验,即随机变量服从二项分布
,再与参考数据比较得是否有把握(2)有放回事件,可看作为独立重复试验,即随机变量服从二项分布![]() ,根据二项分布公式求分布列及数学期望
,根据二项分布公式求分布列及数学期望
试题解析:解:(Ⅰ)由题意得列联表:
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | 60 | 100 | 160 |
外语不优秀 | 140 | 500 | 640 |
总计 | 200 | 600 | 800 |
因为![]() ,由
,由![]() 知,有
知,有![]() 的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”.
的把握认为“该校学生语文成绩优秀与外语成绩是否优秀有关系”.
(Ⅱ)由已知得,随机抽取1名学生,其语文、外语两科成绩至少有一科优秀的概率是![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足
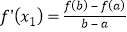
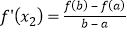 , ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
, ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.( ,
, )
)
B.( ,3)
,3)
C.( , 1)
, 1)
D.( , 1)
, 1) -
科目: 来源: 题型:
查看答案和解析>>【题目】某农户计划建造一个室内面积为800m2的矩形蔬菜温室,在温室外,沿左、右两侧与后侧各保留1m宽的通道,沿前侧保留3m的空地(如图所示),当矩形温室的长和宽分别为多少时,总占地面积最大?并求出最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x||x+1|<4},B={x|(x﹣1)(x﹣2a)<0}.
(1)求A,B;
(2)若A∩B=B,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)对定义域R内的任意x都有f(x)=f(4﹣x),且当x≠2时其导函数f′(x)满足(x﹣2)f′(x)>0,若2<a<4则( )
A.f(2a)<f(3)<f(log2a)
B.f(log2a)<f(3)<f(2a)
C.f(3)<f(log2a)<f(2a)
D.f(log2a)<f(2a)<f(3) -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b∈R,ab≠0,给出下面四个命题:①a2+b2≥﹣2ab;②
 ≥2;③若a<b,则ac2<bc2;④若
≥2;③若a<b,则ac2<bc2;④若  .则a>b;其中真命题有( )
.则a>b;其中真命题有( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
 =
=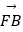 ,
,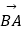

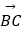 =48,则抛物线的方程为( )
=48,则抛物线的方程为( )
A.y2=4x
B.y2=8x
C.y2=16x
D.y2=4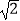 X
X
相关试题

