【题目】如图,在平面直角坐标系![]() 中,设点
中,设点![]() 是椭圆
是椭圆![]() :
: ![]() 上一点,从原点
上一点,从原点![]() 向圆
向圆![]() :
: ![]() 作两条切线分别与椭圆
作两条切线分别与椭圆![]() 交于点
交于点![]() ,
, ![]() ,直线
,直线![]() ,
, ![]() 的斜率分别记为
的斜率分别记为![]() ,
, ![]() .
.

(1)求证: ![]() 为定值;
为定值;
(2)求四边形![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)证明见解析;(2)1.
【解析】试题分析:(1)因为直线![]() :
: ![]() ,
, ![]() :
: ![]() ,与圆
,与圆![]() 相切,推出
相切,推出![]() ,
, ![]() 是方程
是方程![]() 的两个不相等的实数根,利用韦达定理得
的两个不相等的实数根,利用韦达定理得![]() ,结合点点
,结合点点![]() 在椭圆
在椭圆![]() 上,得出
上,得出![]() ;(2)当直线
;(2)当直线![]() ,
, ![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
, ![]() ,通过
,通过![]() ,推出
,推出![]() ,结合
,结合![]() ,
, ![]() 在椭圆
在椭圆![]() 上,可得
上,可得![]() ,再讨论直线落在坐标轴上时,显然有
,再讨论直线落在坐标轴上时,显然有![]() ,然后表示出
,然后表示出![]() ,结合基本不等式即可求出四边形
,结合基本不等式即可求出四边形![]() 面积的最大值.
面积的最大值.
试题解析:(1)因为直线![]() :
: ![]() ,
, ![]() :
: ![]() ,与圆
,与圆![]() 相切,
相切,
由 ,可得
,可得![]() ,
, ![]() 是方程
是方程![]() 的两个不相等的实数根
的两个不相等的实数根
∴![]() ,因为点
,因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
∴![]() .
.
(2)(i)当直线![]() ,
, ![]() 不落在坐标轴上时,设
不落在坐标轴上时,设![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
因为![]() ,
, ![]() 在椭圆
在椭圆![]() 上,
上,
所以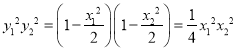 ,
,
整理得![]() ,所以
,所以![]() ,
,
所以![]() .
.
(ii)当直线落在坐标轴上时,显然有![]() ,
,
综上: ![]() .
.
因为![]() ,
,
因为![]() ,
,
所以![]() 的最大值为1.
的最大值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是
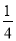 ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为
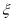 ,求
,求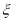 的分布列及
的分布列及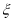 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
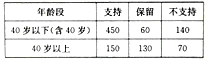
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
-
科目: 来源: 题型:
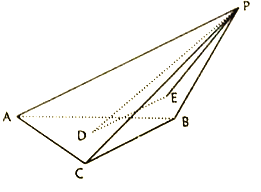
查看答案和解析>>【题目】如图,在三棱锥
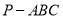 中,
中, 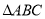 是正三角形,面
是正三角形,面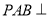 面
面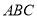 ,
, 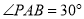 ,
, 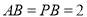 ,
, 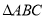 和
和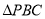 的重心分别为
的重心分别为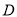 ,
, 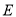 .
.
(1)证明:
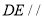 面
面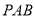 ;
;(2)求
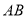 与面
与面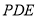 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
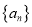 满足:
满足: 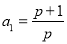 ,
, 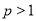 ,
, 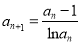 .
. (1)证明:
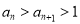 ;
;(2)证明:
 ;
;(3)证明:
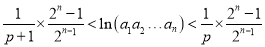 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 底面
底面 ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且 .
.
(Ⅰ)若点
 为
为 上一点且
上一点且 ,证明:
,证明: 平面
平面 ;
;(Ⅱ)求二面角
 的大小;
的大小;(Ⅲ)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由.
的长;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数数列
 满足
满足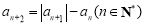 ,则称数列
,则称数列 为“
为“ 数列”.
数列”.(Ⅰ)若数列
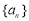 是
是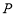 数列,且
数列,且 ,求
,求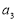 ,
, 的值;
的值;(Ⅱ)求证:若数列
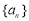 是
是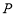 数列,则
数列,则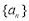 的项不可能全是正数,也不可能全是负数;
的项不可能全是正数,也不可能全是负数;(Ⅲ)若数列
 为
为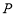 数列,且
数列,且 中不含值为零的项,记
中不含值为零的项,记 前
前 项中值为负数的项的个数为
项中值为负数的项的个数为 ,求
,求 所有可能取值.
所有可能取值.
相关试题

