【题目】已知函数![]() .
.
(1)解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,其中
,其中![]() 为奇函数,
为奇函数,![]() 为偶函数,若不等式
为偶函数,若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用换元法,将原不等式转化为一元二次不等式来求解.(2)将问题分离常数,转化为![]() 在
在![]() 有解的问题来解决.求得
有解的问题来解决.求得![]() 在
在![]() 上的值域,来求得
上的值域,来求得![]() 的取值范围.(3)先根据函数的奇偶性的概念,求得
的取值范围.(3)先根据函数的奇偶性的概念,求得![]() 的解析式,化简所求不等式为
的解析式,化简所求不等式为![]() ,利用换元法及分离参数法分离出
,利用换元法及分离参数法分离出![]() ,利用恒成立问题解决方法求得
,利用恒成立问题解决方法求得![]() 的取值范围.
的取值范围.
(1)原不等式即为![]() ,设t=2x,则不等式化为t﹣t2>16﹣9t,
,设t=2x,则不等式化为t﹣t2>16﹣9t,
即t2﹣10t+16<0,解得![]() ,即
,即![]() ,∴1<x<3,∴原不等式的解集为
,∴1<x<3,∴原不等式的解集为![]() .
.
(2)函数![]() 在
在![]() 上有零点,∴
上有零点,∴![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 有解.
有解.
设![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() .∵
.∵![]() 在
在![]() 有解,∴
有解,∴![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]() .
.
(3)由题意得![]() ,解得
,解得 .
.
由题意得![]() ,
,
即![]()
对任意![]() 恒成立,令
恒成立,令![]() ,
,![]() ,则
,则![]() .
.
则得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() .
.
∴![]() ,∴实数
,∴实数![]() 的取值范围
的取值范围![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣9x,函数g(x)=3x2+a.
(1)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;
(2)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知
 两学习小组各有
两学习小组各有 位同学,每位同学在两场讲座任意选听一场.若
位同学,每位同学在两场讲座任意选听一场.若 组
组 人选听《生活趣味数学》,其余
人选听《生活趣味数学》,其余 人选听《校园舞蹈赏析》;
人选听《校园舞蹈赏析》; 组
组 人选听《生活趣味数学》,其余
人选听《生活趣味数学》,其余 人选听《校园舞蹈赏析》.
人选听《校园舞蹈赏析》.(1)若从此
 人中任意选出
人中任意选出 人,求选出的
人,求选出的 人中恰有
人中恰有 人选听《校园舞蹈赏析》的概率;
人选听《校园舞蹈赏析》的概率;(2)若从
 两组中各任选
两组中各任选 人,设
人,设 为选出的
为选出的 人中选听《生活趣味数学》的人数,求
人中选听《生活趣味数学》的人数,求 的分布列.
的分布列. -
科目: 来源: 题型:
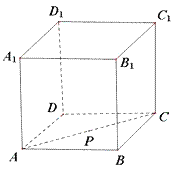
查看答案和解析>>【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
①D1P∥平面A1BC1;
②D1P⊥BD;
③平面PDB1⊥平面A1BC1;
④三棱锥A1﹣BPC1的体积不变.
则其中所有正确的命题的序号是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左、右顶点分别为A,B,直线l斜率大于0,且l经过椭圆的右焦点F,与椭圆交于两点P,Q,若△AFP,△BFQ的面积分别为S1,S2,若
的左、右顶点分别为A,B,直线l斜率大于0,且l经过椭圆的右焦点F,与椭圆交于两点P,Q,若△AFP,△BFQ的面积分别为S1,S2,若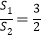 ,则直线l的斜率为_____.
,则直线l的斜率为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为棱AB,BC的中点,点F在侧棱B1B上,且B1E⊥C1F,A1C1⊥B1C1.
(1)求证:DE∥平面A1C1F;
(2)求证:B1E⊥平面A1C1F

相关试题

