
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)判断并说明函数![]() 的零点个数.若函数
的零点个数.若函数![]() 所有零点均在区间
所有零点均在区间![]() 内,求
内,求![]() 的最小值.
的最小值.
【答案】(1)函数![]() 的单调增区间为
的单调增区间为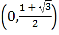 ,单调减区间为
,单调减区间为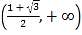 (2)
(2)![]() 存在两个零点,详见解析;
存在两个零点,详见解析; ![]() 的最小值为3
的最小值为3
【解析】
(1)求出导函数![]() ,由
,由![]() 确定增区间,由
确定增区间,由![]() 确定减区间;
确定减区间;
(2)求出导函数![]() ,分类讨论
,分类讨论![]() 的正负,确定
的正负,确定![]() 的单调性,再根据零点存在定理确定零点存在的区间.首先确定
的单调性,再根据零点存在定理确定零点存在的区间.首先确定![]() 上有一个零点,然后确定
上有一个零点,然后确定![]() ,
,![]() ,
,![]() ,
,![]() 上有否零点,从而可得
上有否零点,从而可得![]() 的最小值.
的最小值.
解:(1)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ,
,![]() (舍).
(舍).
当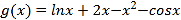 时,
时,![]() ,当
,当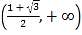 时,
时,![]() ,
,
所以![]() 在
在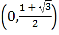 上单调递增,在
上单调递增,在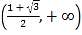 上单调递减,
上单调递减,
因此,函数![]() 的单调增区间为
的单调增区间为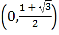 ,单调减区间为
,单调减区间为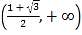 .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,
,
因为![]() 单调递减,
单调递减,
所以![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() .
.
当![]() ,
,![]() ,
,![]() ,
,
所以![]() 单调递减,
单调递减,
又![]() ,
,
所以![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,所以
,所以![]() ,故不存在零点.
,故不存在零点.
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 单调递减,
单调递减,
又![]() ,
,![]() ,
,
所以存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
又![]() ,
,![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,故不存在零点.
,故不存在零点.
综上,![]() 存在两个零点
存在两个零点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
因此![]() 的最小值为3.
的最小值为3.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】某商店举行促销反馈活动,顾客购物每满200元,有一次抽奖机会(即满200元可以抽奖一次,满400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为1,2,3,4,5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如1,2,5),则获得一等奖,奖金40元;若摸得的小球编号一次比一次小(如5,3,1),则获得二等奖,奖金20元;其余情况获得三等奖,奖金10元.
(1)某人抽奖一次,求其获奖金额X的概率分布和数学期望;
(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆节假期期间,某商场为掌握假期期间顾客购买商品人次,统计了10月1日7:00-23:00这一时间段内顾客0这一时间段内顾客购买商品人次,统计发现这一时间段内顾客购买商品共5000人次顾客购买商品时刻的频率分布直方图如下图所示,其中时间段7:00 11:00,11:00 15:00,15:00 ~19:00,19:00~23:00,依次记作[7,11),[11,15),[15,19),[19,23].
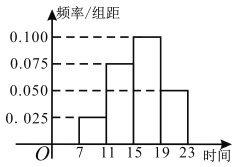
(1)求该天顾客购买商品时刻的中位数t与平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)现从10月1日在该商场购买商品的顾客中随机抽取100名顾客,经统计有男顾客 40人,其中10人购物时刻在[19,23](夜晚),女顾客60人,其中50人购物时刻在[7,19)(白天),根据提供的统计数据,完成下面的2×2列联表,并判断是否有90%的把握认为“男顾客更喜欢在夜晚购物”?
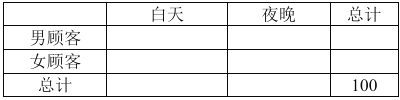
附:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)对该快递点近![]() 天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为
天的每日揽包裹数(单位:件)进行统计,得到的日揽包裹数分别为![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,
件,![]() 件,那么从这
件,那么从这![]() 天中随机抽出
天中随机抽出![]() 天,求这
天,求这![]() 天的日揽包裹数均超过
天的日揽包裹数均超过![]() 件的概率.
件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() 通过
通过![]() 以直线
以直线![]() 为轴顺时针旋转
为轴顺时针旋转![]() 得到(
得到(![]() ).点
).点![]() 为斜边
为斜边![]() 上一点.点
上一点.点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角取最大值时,求二面角
所成的角取最大值时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,准线为l,AB为过焦点F且垂直于x轴的抛物线C的弦,已知以AB为直径的圆经过点(-1,0).
(1)求p的值及该圆的方程;
(2)设M为l上任意一点,过点M作C的切线,切点为N,证明:MF⊥NF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com