【题目】某纪念章从2016年10月1日起开始上市,通过市场调查,得到该纪念章每1枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 | 4 | 10 | 36 |
市场价 | 90 | 51 | 90 |
(1)根据上表数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系并说明理由:①
的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() .
.
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
参考答案:
【答案】(1)②![]() ;(2)上市
;(2)上市![]() 天时,最低价为
天时,最低价为![]() .
.
【解析】
试题分析:(1)随着时间![]() 的增加,
的增加,![]() 的值先减后增,①③为单调函数,所以选②;(2)把点
的值先减后增,①③为单调函数,所以选②;(2)把点![]() 代入
代入![]() 中,解出
中,解出![]() ,利用配方法求得函数当
,利用配方法求得函数当![]() 时取得最小值为
时取得最小值为![]() .
.
试题解析:
(1)∵随着时间![]() 的增加,
的增加,![]() 的值先减后增,
的值先减后增,
而所给的三个函数中![]() 和
和![]() 显然都是单调函数,不满足题意,
显然都是单调函数,不满足题意,
∴选择![]() .………………………………6分
.………………………………6分
(2)把点![]() 代入
代入![]() 中,
中,
得 ,………………………………8分
,………………………………8分
解得![]() .…………………………10分
.…………………………10分
∴![]() ,………………11分
,………………11分
∴当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
答:当纪念章上市20天时,该纪念章的市场价最低,最低市场价为26元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在回归分析中,
 为0.98的模型比
为0.98的模型比 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
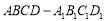 中,棱长
中,棱长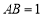 ,过点
,过点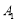 的平面
的平面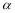 与正方体的面相交,交线围成一个正三角形.
与正方体的面相交,交线围成一个正三角形.
(1)在图中画出这个正三角形(不必说明画法和理由);
(2)平面
 将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
将该正方体截成两个几何体,求体积较大的几何体的体积和表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是偶函数.
是偶函数.(1)求
 的值;
的值;(2)若函数
 ,是否存在实数
,是否存在实数 使得
使得 最小值为0,若存在,求出
最小值为0,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】三段论推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是 .(填写序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数是奇函数且在定义域内是增函数的是( )
A. y=ex B. y=tanx C. y=lnx D. y=x3+x
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据统计图的数据,下列结论错误的是( )
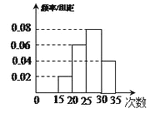
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约有320人
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约有32人
相关试题

