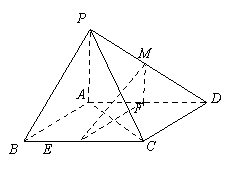
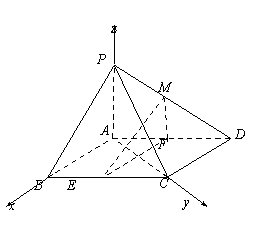
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)详见解析;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)要证明线与面垂直,根据判定定理,需要证明线与平面内的两条相交直线垂直,根据中点易证明![]() ,所以可以将问题转化为证明
,所以可以将问题转化为证明![]() 与平面
与平面![]() 内的两条相交直线垂直,即证明
内的两条相交直线垂直,即证明![]() 和
和![]() ;
;
(Ⅱ)根据上一问所证明的垂直关系,可以建立以![]() 为原点的空间直角坐标系,设
为原点的空间直角坐标系,设![]() ,根据
,根据![]() ,表示点
,表示点![]() 的坐标,首先求平面
的坐标,首先求平面![]() 的法向量
的法向量![]() ,以及平面
,以及平面![]() 的法向量
的法向量![]() ,并根据
,并根据![]() 建立方程,求
建立方程,求![]() .
.
试题解析:(Ⅰ)证明:在平行四边形![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() .
.
由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() ,
,
所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,
,
所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 两两垂直,故以
两两垂直,故以![]()
分别为![]() 轴、
轴、![]() 轴和
轴和![]() 轴,如上图建立空间直角坐标系,
轴,如上图建立空间直角坐标系,
则![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
易得平面![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得![]()
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即![]() ,
,
所以 ![]() ,
,
解得![]() ,或
,或![]() (舍).
(舍).
综上所得:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的方程为
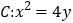 ,过点
,过点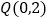 的一条直线与抛物线
的一条直线与抛物线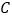 交于
交于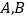 两点,若抛物线在
两点,若抛物线在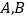 两点的切线交于点
两点的切线交于点 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)设直线
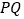 与直线
与直线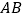 的夹角为
的夹角为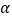 ,求
,求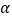 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:y=x+1,圆O:
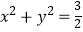 ,直线l被圆截得的弦长与椭圆C:
,直线l被圆截得的弦长与椭圆C: 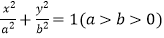 的短轴长相等,椭圆的离心率e=
的短轴长相等,椭圆的离心率e= 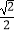 .
.
(1)求椭圆C的方程;
(2)过点M(0,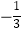 )的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由.
)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过定点T?若存在,求出点T的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
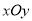 中,直线
中,直线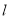 的参数方程为
的参数方程为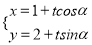 (
(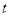 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系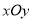 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以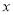 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆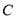 的方程为
的方程为 .
.(1)求圆
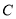 的直角坐标方程;
的直角坐标方程;(2)设圆
 与直线
与直线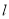 交于点
交于点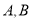 ,若点
,若点 的坐标为
的坐标为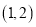 ,求
,求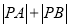 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件
 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件 发生的概率;
发生的概率;(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量
 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017重庆二诊】已知函数
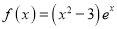 ,设关于
,设关于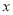 的方程
的方程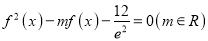 有
有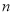 个不同的实数解,则
个不同的实数解,则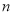 的所有可能的值为( )
的所有可能的值为( )A. 3 B. 1或3 C. 4或6 D. 3或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017河北唐山三模】已知函数
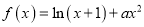 ,
, 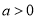 .
.(1)讨论函数
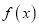 的单调性;
的单调性;(2)若函数
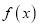 在区间
在区间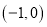 有唯一零点
有唯一零点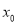 ,证明:
,证明: 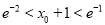 .
.
相关试题

