【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值和单调区间;
的极值和单调区间;
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)极小值是![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数求解;(2)先借助导数分类讨论求出最值,再建立不等式求解.
试题解析:
(1)当![]() ,
,
令![]() ,得
,得![]() ,
,
又![]() 的定义域为
的定义域为![]() ,由
,由![]() 得
得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 时,
时,![]() 有极小值为1,
有极小值为1,
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() ,且
,且![]() ,令
,令![]() ,得到
,得到![]() ,若在区间
,若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,即
成立,即![]() 在区间
在区间![]() 上的最小值小于0.
上的最小值小于0.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
当![]() ,即
,即![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于0不成立,
上的最小值小于0不成立,
②若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() ,
,
综上,由①②可知:![]() 符合题意.
符合题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
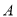 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批 产品所需原材料减少了
产品所需原材料减少了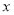 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了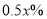 ;若将少用的
;若将少用的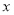 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的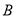 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为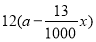 万元,其中
万元,其中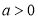 .
.(1)若设备升级后生产这批
 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批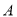 产品的利润,求
产品的利润,求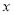 的取值范围;
的取值范围;(2)若生产这批
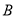 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批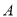 产品的利润,求
产品的利润,求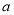 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组
频数
频率

5

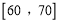
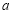
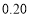
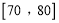
35
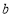
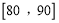
25
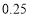
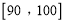
15
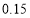
合计
100
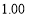
(Ⅰ)求
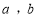 的值及随机抽取一考生恰为优秀生的概率;
的值及随机抽取一考生恰为优秀生的概率;(Ⅱ)按成绩采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在
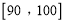 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 ,底面
,底面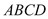 为直角梯形,
为直角梯形,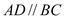 ,
,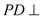 底面
底面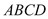 ,
,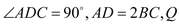 为
为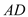 的中点,
的中点,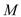 为棱
为棱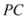 的中点.
的中点.(Ⅰ)证明:
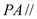 平面
平面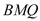 ;
;(Ⅱ)已知
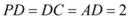 ,求点
,求点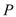 到平面
到平面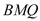 的距离.
的距离.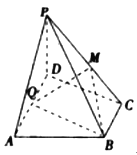
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足{1}X{1,2,3,4}的集合X有( )
A.4个B.5个C.6个D.7个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批 产品所需原材料减少了
产品所需原材料减少了 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了 ;若将少用的
;若将少用的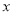 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为 万元,其中
万元,其中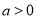 .
.(1)若设备升级后生产这批
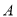 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批 产品的利润,求
产品的利润,求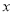 的取值范围;
的取值范围;(2)若生产这批
 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批 产品的利润,求
产品的利润,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平面
平面 ,
, ,
, ,
, 为
为 中点.
中点.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的正弦值;
的正弦值;(3)求点
 到平面
到平面 的距离.
的距离.
相关试题

