【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
参考答案:
【答案】(1)![]() ;(2)定点
;(2)定点![]()
【解析】试题分析:(1)利用点斜式设直线直线![]() 的方程,与抛物线联立方程组,结合韦达定理与弦长公式求
的方程,与抛物线联立方程组,结合韦达定理与弦长公式求![]() ,再根据
,再根据![]() 解得
解得![]() .(2)先设直线
.(2)先设直线![]() 方程
方程![]() , 与抛物线联立方程组,结合韦达定理化简
, 与抛物线联立方程组,结合韦达定理化简![]() ,得
,得![]() 或
或![]() ,代入
,代入![]() 方程可得直线
方程可得直线![]() 过定点
过定点![]()
试题解析:(1)拋物线的焦点![]() ,∴直线
,∴直线![]() 的方程为:
的方程为: ![]() .
.
联立方程组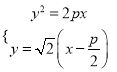 ,消元得:
,消元得: ![]() ,
,
∴![]() .
.
∴![]()
解得![]() .
.
∴抛物线![]() 的方程为:
的方程为: ![]() .
.
(2)由(1)可得点![]() ,可得直线
,可得直线![]() 的斜率不为0,
的斜率不为0,
设直线![]() 的方程为:
的方程为: ![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ①.
①.
设![]() ,则
,则![]() .
.
∵![]()
![]()
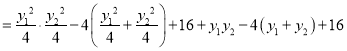
![]()
![]()
即![]() ,得:
,得: ![]() ,
,
∴![]() ,即
,即![]() 或
或![]() ,
,
代人①式检验均满足![]() ,
,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
∴直线过定点![]() (定点
(定点![]() 不满足题意,故舍去).
不满足题意,故舍去).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为 的椭圆
的椭圆 的一个焦点为圆
的一个焦点为圆 :
:  的圆心.
的圆心.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设
 是椭圆
是椭圆 上一点,过
上一点,过 作两条斜率之积为
作两条斜率之积为 的直线
的直线 ,
,  ,当直线
,当直线 ,
,  都与圆
都与圆 相切时,求
相切时,求 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,某市实验中学校领导审时度势,深化教育教学改革,经过师生共同努力,高考成绩硕果累累,捷报频传,尤其是2017年某著名高校在全国范围内录取的大学生中就有25名来自该中学.下表为该中学近5年被录取到该著名高校的学生人数.(记2013年的年份序号为1,2014年的年份序号为2,依此类推……)
年份序号

1
2
3
4
5
录取人数

10
13
17
20
25
(1)求
 关于
关于 的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);
的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);(2)若在第1年和第4年录取的大学生中按分层抽样法抽取6人,再从这6人中任选2人,求这2人中恰好有一位来自第1年的概率.
参考数据:
 ,
, .
.参考公式:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业里工人的工资与其生产利润满足线性相关关系,现统计了100名工人的工资
 (元)与其生产利润
(元)与其生产利润 (千元)的数据,建立了
(千元)的数据,建立了 关于
关于 的回归直线方程为
的回归直线方程为 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 工人甲的生产利润为1000元,则甲的工资为130元
B. 生产利润提高1000元,则预计工资约提高80元
C. 生产利润提高1000元,则预计工资约提高130元
D. 工人乙的工资为210元,则乙的生产利润为2000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段
 ,
, ,
, ,
, ,
, ,
, 进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,则得到体育成绩的折线图如下:
进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,则得到体育成绩的折线图如下:
(1)若体育成绩大于或等于70分的学生为“体育良好”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良好”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为
 ,且
,且 ,
, ,
, ,当三人的体育成绩方差
,当三人的体育成绩方差 最小时,写出
最小时,写出 的所有可能取值(不要求证明)
的所有可能取值(不要求证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2,
 .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
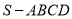 中,平面
中,平面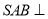 平面
平面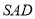 ,侧面
,侧面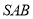 是边长为
是边长为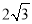 的等边三角形,底面
的等边三角形,底面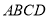 是矩形,且
是矩形,且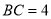 ,则该四棱锥外接球的表面积等于__________.
,则该四棱锥外接球的表面积等于__________.
相关试题

