【题目】在直角坐标系![]() 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为![]() 的椭圆
的椭圆![]() 的一个焦点为圆
的一个焦点为圆![]() :
: ![]() 的圆心.
的圆心.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,过
上一点,过![]() 作两条斜率之积为
作两条斜率之积为![]() 的直线
的直线![]() ,
, ![]() ,当直线
,当直线![]() ,
, ![]() 都与圆
都与圆![]() 相切时,求
相切时,求![]() 的坐标.
的坐标.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() ,或
,或![]() ,或
,或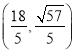 ,或
,或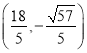 .
.
【解析】试题分析:(1)圆心坐标是已知的,故椭圆的焦点是已知的,从而半焦距![]() 已知了,又有离心率,故半长轴长
已知了,又有离心率,故半长轴长![]() 也能求出,从而求出
也能求出,从而求出![]() ,而根据题意,椭圆方程是标准方程,可其方程易得;(2)设P点坐标为
,而根据题意,椭圆方程是标准方程,可其方程易得;(2)设P点坐标为![]() ,再设一条切线的斜率为
,再设一条切线的斜率为![]() ,则另一条切线的斜率为
,则另一条切线的斜率为![]() ,三个未知数
,三个未知数![]() 需要三个方程,点P在椭圆上,一个等式,两条直线都圆的切线,利用圆心到切线的距离等于圆的半径又得到两个等式,三个等量关系,三个未知数理论上可解了,当然具体解题时,可设切线斜率为
需要三个方程,点P在椭圆上,一个等式,两条直线都圆的切线,利用圆心到切线的距离等于圆的半径又得到两个等式,三个等量关系,三个未知数理论上可解了,当然具体解题时,可设切线斜率为![]() ,则点斜率式写出直线方程,利用圆心到切线距离等于圆半径得出关于
,则点斜率式写出直线方程,利用圆心到切线距离等于圆半径得出关于![]() 的方程,而
的方程,而![]() 是这个方程的两解,由韦达定理得
是这个方程的两解,由韦达定理得![]() ,这个结果又是
,这个结果又是![]() ,就列出了关于P点坐标的一个方程,再由P点在椭圆上,可解出P点坐标.
,就列出了关于P点坐标的一个方程,再由P点在椭圆上,可解出P点坐标.
试题解析:(1)圆的标准方程为![]() ,圆心为
,圆心为![]() ,所以
,所以![]() ,又
,又![]() ,
, ![]() ,
, ![]() ,而据题意椭圆的方程是标准方程,故其方程为
,而据题意椭圆的方程是标准方程,故其方程为![]() .4分
.4分
(2)设![]() ,得
,得![]()
∵![]() ,依题意
,依题意![]() 到
到![]() 的距离为
的距离为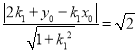
整理得![]() 同理
同理
![]()
∴![]() 是方程
是方程![]() 的两实根10分
的两实根10分
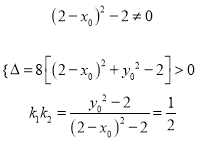 12分
12分
∴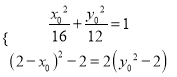 14分
14分
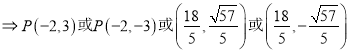 16分
16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
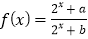 .
.(1)当
 ,
, 时,求满足
时,求满足 的
的 的值;
的值;(2)若函数
 是定义在
是定义在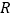 上的奇函数.
上的奇函数. ①存在
 ,使得不等式
,使得不等式 有解,求实数
有解,求实数 的取值范围;
的取值范围;②若函数
 满足
满足 ,若对任意
,若对任意 且
且 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 的前
的前 项和为
项和为 ,
, ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)设数列
 满足:
满足:对于任意
 ,都有
,都有 成立.
成立.①求数列
 的通项公式;
的通项公式;②设数列
 ,问:数列
,问:数列 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.
(1)求取到的2个球中恰好有1个是黑球的概率;
(2)求取到的2个球中至少有1个是红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,某市实验中学校领导审时度势,深化教育教学改革,经过师生共同努力,高考成绩硕果累累,捷报频传,尤其是2017年某著名高校在全国范围内录取的大学生中就有25名来自该中学.下表为该中学近5年被录取到该著名高校的学生人数.(记2013年的年份序号为1,2014年的年份序号为2,依此类推……)
年份序号

1
2
3
4
5
录取人数

10
13
17
20
25
(1)求
 关于
关于 的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);
的线性回归方程,并估计2018年该中学被该著名高校录取的学生人数(精确到整数);(2)若在第1年和第4年录取的大学生中按分层抽样法抽取6人,再从这6人中任选2人,求这2人中恰好有一位来自第1年的概率.
参考数据:
 ,
, .
.参考公式:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业里工人的工资与其生产利润满足线性相关关系,现统计了100名工人的工资
 (元)与其生产利润
(元)与其生产利润 (千元)的数据,建立了
(千元)的数据,建立了 关于
关于 的回归直线方程为
的回归直线方程为 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 工人甲的生产利润为1000元,则甲的工资为130元
B. 生产利润提高1000元,则预计工资约提高80元
C. 生产利润提高1000元,则预计工资约提高130元
D. 工人乙的工资为210元,则乙的生产利润为2000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线
 的焦点
的焦点 ,斜率为
,斜率为 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 .
.(1)求该抛物线
 的方程;
的方程;(2)已知抛物线上一点
 ,过点
,过点 作抛物线的两条弦
作抛物线的两条弦 和
和 ,且
,且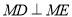 ,判断直线
,判断直线 是否过定点?并说明理由.
是否过定点?并说明理由.
相关试题

