【题目】在平面直角坐标系![]() 中,圆C的参数方程为
中,圆C的参数方程为 ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为![]() .
.
(1)求圆C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P是圆C上任一点,求△PAB面积的最小值.
参考答案:
【答案】(1)圆C的普通方程为![]() ,直线l的直角坐标方程为
,直线l的直角坐标方程为![]() ;(2)4.
;(2)4.
【解析】
试题分析:(1)由![]() 消去参数可得圆的普通方程,由
消去参数可得圆的普通方程,由![]() 可化直线极坐标方程为直角坐标方程;(2)把点
可化直线极坐标方程为直角坐标方程;(2)把点![]() 的极坐标化为直角坐标后,知这两点在直线
的极坐标化为直角坐标后,知这两点在直线![]() ,计算
,计算![]() ,因此只要求得点
,因此只要求得点![]() 到直线
到直线![]() 的距离的最小值即能得
的距离的最小值即能得![]() 面积的最小值.可用点到直线距离公式,也可用几何法求得圆心到直线的距离得最小值.
面积的最小值.可用点到直线距离公式,也可用几何法求得圆心到直线的距离得最小值.
试题解析:(1)由![]()
得![]()
消去参数t,得![]() ,
,
所以圆C的普通方程为![]() .
.
由![]() ,
,
得![]() ,
,
即![]() ,
,
换成直角坐标系为![]() ,
,
所以直线l的直角坐标方程为![]() .
.
(2)![]() 化为直角坐标为
化为直角坐标为![]() 在直线l上,
在直线l上,
并且![]() ,
,
设P点的坐标为![]() ,
,
则P点到直线l的距离为![]()
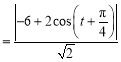 ,
,
![]() ,
,
所以![]() 面积的最小值是
面积的最小值是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x5+ax3+bx-3,若f(-4)=10,则f(4)=( )
A.16
B.-10
C.10
D.-16 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在[m,n]上的奇函数,且f(x)在[m,n]上的最大值为a,则函数F(x)=f(x)+3在[m,n]上的最大值与最小值之和为( )
A.2a+3
B.2a+6
C.6-2a
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如(1)图所示,在直角梯形ABCD中,AD∥BC,
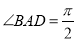 ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.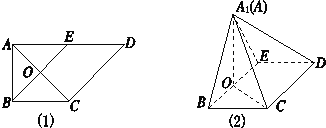
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)证明函数
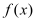 在
在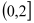 上是减函数,
上是减函数, 上是增函数;
上是增函数;(2)若方程
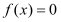 有且只有一个实数根,判断函数
有且只有一个实数根,判断函数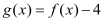 的奇偶性;
的奇偶性;(3)在(2)的条件下探求方程
 的根的个数.
的根的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
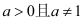 ,函数
,函数 ,
,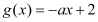 .
.(1)指出
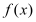 的单调性(不要求证明);
的单调性(不要求证明);(2)若有
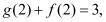 求
求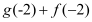 的值;
的值;(3)若
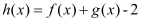 ,求使不等式
,求使不等式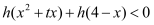 恒成立的
恒成立的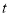 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
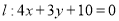 ,半径为
,半径为 的圆
的圆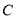 与
与 相切,圆心
相切,圆心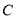 在
在 轴上且在直线
轴上且在直线 的右上方.
的右上方.(1)求圆的方程;
(2)若直线过点
 且与圆
且与圆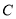 交于
交于 两点(
两点( 在
在 轴上方,B在
轴上方,B在 轴下方),问在
轴下方),问在 轴正半轴上是否存在定点
轴正半轴上是否存在定点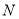 ,使得
,使得 轴平分
轴平分 ?若存在,请求出点
?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

