【题目】已知直线![]() ,半径为
,半径为![]() 的圆
的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点![]() 且与圆
且与圆![]() 交于
交于![]() 两点(
两点(![]() 在
在![]() 轴上方,B在
轴上方,B在![]() 轴下方),问在
轴下方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)当点
(2)当点![]()
![]() 时, 能使得
时, 能使得![]() 总成立
总成立
【解析】
试题分析:(1)设出圆心C坐标,根据直线l与圆C相切,得到圆心到直线l的距离d=r,确定出圆心C坐标,即可得出圆C方程;(2)当直线AB⊥x轴,则x轴平分∠ANB,当直线AB斜率存在时,设直线AB方程为y=k(x-1),联立圆与直线方程,消去y得到关于x的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若x轴平分∠ANB,则kAN=-kBN,求出t的值,确定出此时N坐标即可
试题解析:(1)设圆心![]() ,则
,则![]() 或
或![]() (舍).所以圆
(舍).所以圆![]() .
.
(2)当直线![]() 轴时,
轴时,![]() 轴平分
轴平分![]() ,当直线
,当直线![]() 的斜率存在时, 设直线
的斜率存在时, 设直线![]() 的方程为
的方程为![]() ,由
,由 得,
得,![]() , 若
, 若![]() 轴平分
轴平分![]() ,则
,则![]()
![]()
![]() ,所以当点
,所以当点![]()
![]() 时, 能使得
时, 能使得![]() 总成立.
总成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,圆C的参数方程为
中,圆C的参数方程为 ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线 的极坐标方程为
的极坐标方程为 ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为 .
.(1)求圆C的普通方程和直线
 的直角坐标方程;
的直角坐标方程;(2)点P是圆C上任一点,求△PAB面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)证明函数
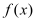 在
在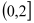 上是减函数,
上是减函数, 上是增函数;
上是增函数;(2)若方程
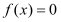 有且只有一个实数根,判断函数
有且只有一个实数根,判断函数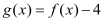 的奇偶性;
的奇偶性;(3)在(2)的条件下探求方程
 的根的个数.
的根的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
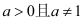 ,函数
,函数 ,
,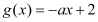 .
.(1)指出
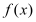 的单调性(不要求证明);
的单调性(不要求证明);(2)若有
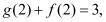 求
求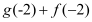 的值;
的值;(3)若
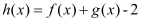 ,求使不等式
,求使不等式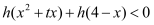 恒成立的
恒成立的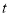 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x),x∈(-a,a),F(x)=f(x)+f(-x),则F(x)是( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
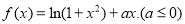
(1)若
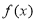 在
在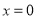 处取得极值,求
处取得极值,求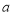 的值;
的值;(2)讨论
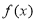 的单调性;
的单调性;(3)证明:
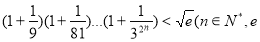 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编为1~50号,并进行分组,第一组1~5号,第二组6~10号,…,第十组46~50号.若在第三组中抽得号码为12的学生,则在第九组中抽得号码为_____的学生.
相关试题

