【题目】已知函数g(x)=ax2﹣2ax+b+1(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)= ![]() .
.
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
参考答案:
【答案】
(1)解:函数g(x)=ax2﹣2ax+b+1=a(x﹣1)2+1+b﹣a,
因为a>0,所以g(x)在区间[2,3]上是增函数,故 ![]() ,解得
,解得 ![]()
(2)解:由已知可得f(x)=x+ ![]() ﹣2,所以,不等式f(2x)﹣k2x≥0可化为 2x+
﹣2,所以,不等式f(2x)﹣k2x≥0可化为 2x+ ![]() ﹣2≥k2x,
﹣2≥k2x,
可化为 1+ ![]() ﹣2
﹣2 ![]() ≥k,令t=
≥k,令t= ![]() ,则 k≤t2﹣2t+1.
,则 k≤t2﹣2t+1.
因 x∈[﹣1,1],故 t∈[ ![]() ,2].故k≤t2﹣2t+1在t∈[
,2].故k≤t2﹣2t+1在t∈[ ![]() ,2]上能成立.
,2]上能成立.
记h(t)=t2﹣2t+1,因为 t∈[ ![]() ,2],故 h(t)max =h(2)=1,
,2],故 h(t)max =h(2)=1,
所以k的取值范围是(﹣∞,1]
【解析】(1)由函数g(x)=a(x﹣1)2+1+b﹣a,a>0,所以g(x)在区间[2,3]上是增函数,故 ![]() ,由此解得a、b的值.(2)不等式可化为 2x+
,由此解得a、b的值.(2)不等式可化为 2x+ ![]() ﹣2≥k2x , 故有 k≤t2﹣2t+1,t∈[
﹣2≥k2x , 故有 k≤t2﹣2t+1,t∈[ ![]() ,2],求出h(t)=t2﹣2t+1的最大值,从而求得k的取值范围.
,2],求出h(t)=t2﹣2t+1的最大值,从而求得k的取值范围.
【考点精析】通过灵活运用二次函数在闭区间上的最值和函数的零点与方程根的关系,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点即可以解答此题.
;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=4x,且f(0)=1.
(1)求二次函数f(x)的解析式.
(2)求函数g(x)=( )f(x)的单调增区间和值域.
)f(x)的单调增区间和值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(x3﹣1)2+1,下列结论中正确的是( )
A.x=1是函数f(x)的极小值点,x=0是函数f(x)的极大值点
B.x=1及x=0均是函数f(x)的极大值点
C.x=1是函数f(x)的极大值点,x=0是函数f(x)的极小值点
D.x=1是函数f(x)的极小值点,函数f(x)无极大值点 -
科目: 来源: 题型:
查看答案和解析>>【题目】设点P在曲线
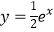 上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
A.1﹣ln2
B.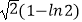
C.1+ln2
D.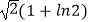
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知z∈C,z+2i 和
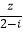 都是实数.
都是实数.
(1)求复数z;
(2)若复数(z+ai)2 在复平面上对应的点在第四象限,求实数a 的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:
30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.
根据上述数据得到样本的频率分布表如下:分组
频数
频率
[25,30]
3
0.12
(30,35]
5
0.20
(35,40]
8
0.32
(40,45]
n1
f1
(45,50]
n2
f2
(1)确定样本频率分布表中n1 , n2 , f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=ax2+bx(a<0)通过点(1,2),且其图象与y=﹣x2+2x的图象有二个交点(如图所示).
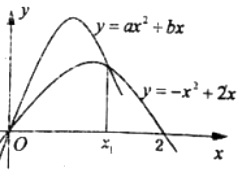
(1)求y=ax2+bx与y=﹣x2+2x所围成的面积S与a的函数关系;
(2)当a,b为何值时,S取得最小值.
相关试题

