【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=4x,且f(0)=1.
(1)求二次函数f(x)的解析式.
(2)求函数g(x)=( ![]() )f(x)的单调增区间和值域.
)f(x)的单调增区间和值域.
参考答案:
【答案】
(1)解:设二次函数f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1.把f(x)的表达式代入f(x+1)﹣f(x)=4x,有
a(x+1)2+b(x+1)+1﹣(ax2+bx+1)=4x.
∴2ax+a+b=4x.∴a=2,b=﹣2.
∴f(x)=2x2﹣2x+1
(2)解:g(x)=( ![]() )f(x)=
)f(x)= ![]() ,
,
令t=2x2﹣2x+1,则t=2x2﹣2x+1=2(x﹣ ![]() )2+
)2+ ![]()
此时y=( ![]() )t为减函数,
)t为减函数,
当x≥ ![]() 时,函数t=2x2﹣2x+1为增函数,此时g(x)为减函数,即函数单调递减区间为(﹣∞,
时,函数t=2x2﹣2x+1为增函数,此时g(x)为减函数,即函数单调递减区间为(﹣∞, ![]() ],
],
当x≤ ![]() 时,函数t=2x2﹣2x+1为减函数,此时g(x)为增函数,即函数单调递增区间为[
时,函数t=2x2﹣2x+1为减函数,此时g(x)为增函数,即函数单调递增区间为[ ![]() ,+∞),
,+∞),
∵t=2x2﹣2x+1=2(x﹣ ![]() )2+
)2+ ![]() ≥
≥ ![]() ,
,
∴0<( ![]() )t≤=(
)t≤=( ![]() )
) ![]() =
= ![]() ,
,
即函数的值域为(0, ![]() ]
]
【解析】(1)利用待定系数法即可求二次函数f(x)的解析式.(2)利用换元法结合复合函数单调性的关系结合一元二次函数和指数函数的性质进行求解即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,a1=
 ,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
(1)写出此数列的前5项;
(2)归纳猜想{an}的通项公式,并用数学归纳法证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
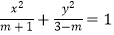 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,
(1)若命题p为真命题,求实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(x3﹣1)2+1,下列结论中正确的是( )
A.x=1是函数f(x)的极小值点,x=0是函数f(x)的极大值点
B.x=1及x=0均是函数f(x)的极大值点
C.x=1是函数f(x)的极大值点,x=0是函数f(x)的极小值点
D.x=1是函数f(x)的极小值点,函数f(x)无极大值点 -
科目: 来源: 题型:
查看答案和解析>>【题目】设点P在曲线
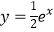 上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
上,点Q在曲线y=ln(2x)上,则|PQ|最小值为( )
A.1﹣ln2
B.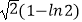
C.1+ln2
D.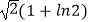
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=ax2﹣2ax+b+1(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)=
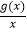 .
.
(1)求a、b的值;
(2)若不等式f(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
相关试题

