【题目】某中学为弘扬优良传统,展示80年来的办学成果,特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者,在众多候选人中选取100名志愿者,为了在志愿者中选拔出节目主持人,现按身高分组,得到的频率分布表如图所示
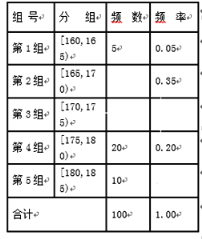
(1)请补充频率分布表中空白位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为选拔出主持人,决定在第3、4、5组中用分层抽样抽取6人上台,求第3、4、5组每组各抽取多少人?
(3)在(2)的前提下,主持人会在上台的6人中随机抽取2人表演诗歌朗诵,求第3组至少有一人被抽取的概率?
参考答案:
【答案】(1)直方图见解析;(2)3,2,1;(3)![]() .
.
【解析】
(1)根第二组的频率计算第二组的频数,再根据总人数得到第三组的频数和频率,从而可补全频率分布表并制作频率分布直方图.
(2)按比例计算各组抽取人数.
(3)用枚举法列出所有的基本事件后用古典概型的概率公式计算即可.
第二组的频数为![]() ,故第三组的频数为
,故第三组的频数为![]() ,故第三组的频率为
,故第三组的频率为![]() ,第五组的频率为
,第五组的频率为![]() ,补全后频率分布表为:
,补全后频率分布表为:
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 | 100 | 1 |
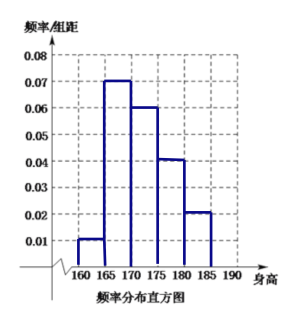
频率分布直方图为:
(2)第三组、第四组、第五组的频率之比![]() ,故第三组、第四组、第五组抽取的人数分别为
,故第三组、第四组、第五组抽取的人数分别为![]() .
.
(3)设第三组中抽取的三人为![]() ,第四组中抽取的两人为
,第四组中抽取的两人为![]() ,第五组中抽取的一人为
,第五组中抽取的一人为![]() ,则6人中任意抽取两人,所有的基本事件如下:
,则6人中任意抽取两人,所有的基本事件如下:
![]() ,
,![]()
故第三组中至少有1人被抽取的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人进行一次围棋比赛,每局胜者得1分,负者得0分,约定一方比另一方多3分或满9局时比赛结束,并规定:只有一方比另一方多三分才算赢,其它情况算平局,假设在每局比赛中,甲获胜的概率为
 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.(1) 求甲获得这次比赛胜利的概率;
(2)设
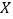 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求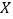 得分布列及数学期望.
得分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】4男3女站成一排,求满足下列条件的排法共有多少种?
 任何两名女生都不相邻,有多少种排法?
任何两名女生都不相邻,有多少种排法? 男甲不在首位,男乙不在末位,有多少种排法?
男甲不在首位,男乙不在末位,有多少种排法? 男生甲、乙、丙顺序一定,有多少种排法?
男生甲、乙、丙顺序一定,有多少种排法? 男甲在男乙的左边
男甲在男乙的左边 不一定相邻
不一定相邻 有多少种不同的排法?
有多少种不同的排法? -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x
6
8
10
12
y
2
3
5
6
参考公式:
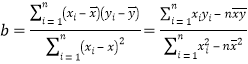
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.
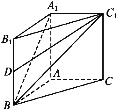
(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
(1)若AF=4,求点A的坐标;
(2)求线段AB的长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
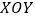 中,以
中,以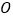 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.己知圆
轴的正半轴为极轴建立极坐标系.己知圆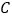 的圆心的坐标为
的圆心的坐标为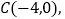 半径为
半径为 ,直线
,直线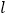 的参数方程为
的参数方程为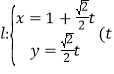 为参数)
为参数) (Ⅰ)求圆C的极坐标方程;直线
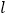 的普通方程;
的普通方程;(Ⅱ)若圆C和直线
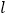 相交于A,B两点,求线段AB的长.
相交于A,B两点,求线段AB的长.
相关试题

