【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.己知圆
轴的正半轴为极轴建立极坐标系.己知圆![]() 的圆心的坐标为
的圆心的坐标为![]() 半径为
半径为![]() ,直线
,直线![]() 的参数方程为
的参数方程为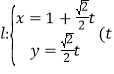 为参数)
为参数)
(Ⅰ)求圆C的极坐标方程;直线![]() 的普通方程;
的普通方程;
(Ⅱ)若圆C和直线![]() 相交于A,B两点,求线段AB的长.
相交于A,B两点,求线段AB的长.
参考答案:
【答案】(Ⅰ) 圆C的极坐标方程为![]() 直线
直线![]() 的普通方程为
的普通方程为![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)根据题干得到圆的标准方程,再通过极坐标和直角坐标的互化得到极坐标方程,通过参数方程得到直线的斜率和定点可得到直线方程;(Ⅱ)计算得到圆心到直线的距离,已知圆的半径,根据勾股定理得到弦长.
(Ⅰ)圆![]() 的圆心的坐标为
的圆心的坐标为![]() 半径为
半径为![]() ,得到圆的一般方程为:
,得到圆的一般方程为:![]() 化为极坐标得到
化为极坐标得到![]() .
.
直线![]() 的参数方程为
的参数方程为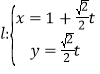 ,可得到直线的斜率为1,过点(1,0),由点斜式得到方程为:
,可得到直线的斜率为1,过点(1,0),由点斜式得到方程为:![]() .
.
(Ⅱ)圆心为(-4,0),圆心到直线的距离为d=![]() 半径为4,由勾股定理得到弦长为
半径为4,由勾股定理得到弦长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为弘扬优良传统,展示80年来的办学成果,特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者,在众多候选人中选取100名志愿者,为了在志愿者中选拔出节目主持人,现按身高分组,得到的频率分布表如图所示
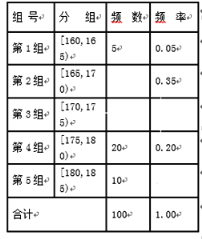
(1)请补充频率分布表中空白位置相应数据,再在答题纸上完成下列频率分布直方图;
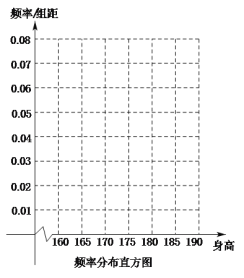
(2)为选拔出主持人,决定在第3、4、5组中用分层抽样抽取6人上台,求第3、4、5组每组各抽取多少人?
(3)在(2)的前提下,主持人会在上台的6人中随机抽取2人表演诗歌朗诵,求第3组至少有一人被抽取的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.
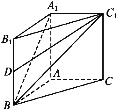
(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A、B两点.
(1)若AF=4,求点A的坐标;
(2)求线段AB的长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现从某学校高一年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于
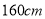 和
和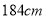 之间,将测量结果按如下方式分成6组:第1组
之间,将测量结果按如下方式分成6组:第1组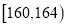 ,第2组
,第2组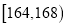 ,…,第6组
,…,第6组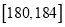 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.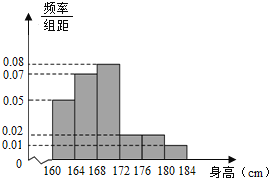
(1)求这50名男生身高的中位数,并估计该校高一全体男生的平均身高;
(2)求这50名男生当中身高不低于176
 的人数,并且在这50名身高不低于176
的人数,并且在这50名身高不低于176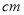 的男生中任意抽取2人,求这2人身高都低于180
的男生中任意抽取2人,求这2人身高都低于180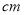 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的中心在原点,一个长轴端点为
 ,离心率
,离心率 ,过P分别作斜率为
,过P分别作斜率为 的直线PA,PB,交椭圆于点A,B。
的直线PA,PB,交椭圆于点A,B。(1)求椭圆的方程;
(2)若
 ,则直线AB是否经过某一定点?
,则直线AB是否经过某一定点? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是
A. 对分类变量X与Y,随机变量K2的观测值k越大,则判断“X与Y有关系”的把握程度越小
B. 在回归直线方程
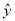 =0.2x+0.8中,当解释变量x每增加1个单位时,预报变量
=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量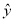 平均增加0.2个单位
平均增加0.2个单位C. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
D. 回归直线过样本点的中心(
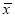 ,
, 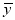 )
)
相关试题

