【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
参考答案:
【答案】(1)a![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】
(1)对原函数求导,根据导数和函数的单调性的关系即可求出![]() 的取值范围;
的取值范围;
(2)问题转化为即![]() 在
在![]() 时恒成立,令
时恒成立,令![]() ,
,![]() 求导后分
求导后分![]() 和
和![]() 求函数的单调区间,进一步求得函数的最值得答案.
求函数的单调区间,进一步求得函数的最值得答案.
解:(1)![]() 函数
函数![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,
![]() 在
在![]() ,
,![]() 上恒成立,
上恒成立,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() (1)
(1)![]() ,
,
![]() 函数
函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() 不等式
不等式![]() 在
在![]() 时恒成立,
时恒成立,
![]() 在
在![]() 时恒成立,
时恒成立,
即![]() 在
在![]() 时恒成立,
时恒成立,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,
上单调递增,
![]() (1)
(1)![]() ,则
,则![]() ,矛盾,
,矛盾,
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
![]() 在
在![]() 单调递减,在
单调递减,在![]() ,
,![]() 单调递增,
单调递增,
![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
![]() ,
,
![]() 不存在整数
不存在整数![]() 使得
使得![]() 恒成立,
恒成立,
综上所述不存在满足条件的整数![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:
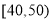 ,
,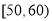 ,
,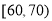 ,
,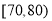 ,
,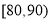 ,
,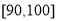 .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表: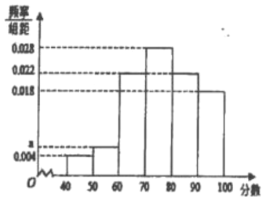
乙教师分数频数分布表
分数区间
频数
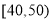
3
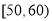
3
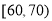
15
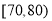
19
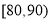
35
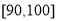
25
(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在
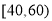 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在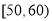 范围内的概率;
范围内的概率;(3)如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中,  分别为
分别为 的中点,点
的中点,点 为线段
为线段 上的一点,将
上的一点,将 沿
沿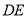 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.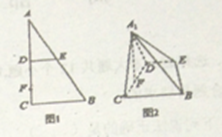
(1)求证:
 ;
;(2)线段
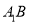 上是否存在点
上是否存在点 ,使
,使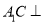 平面
平面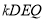 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 上一点
上一点 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为 ,
, 
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过点
 的直线
的直线 交椭圆
交椭圆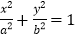 于
于 两点,问在
两点,问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为定值?证明你的结论.
为定值?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
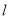 的参数方程为
的参数方程为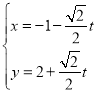 (其中
(其中 为参数),以原点为极点,以
为参数),以原点为极点,以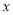 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线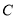 的极坐标方程为
的极坐标方程为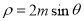 (
( 为常数,且
为常数,且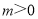 ),直线
),直线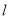 与曲线
与曲线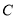 交于
交于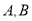 两点.
两点.(1)若
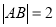 ,求实数
,求实数 的值;
的值;(2)若点
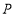 的直角坐标为
的直角坐标为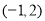 ,且
,且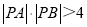 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.
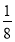 B.
B.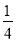 C.
C.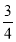 D.
D.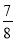
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体
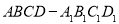 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )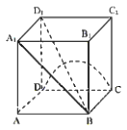
①若P为棱
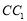 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为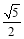 ;
;②若P在线段
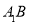 上运动,则
上运动,则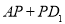 的最小值为
的最小值为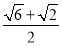 ;
;③若P在半圆弧CD上运动,当三棱锥
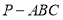 的体积最大时,三棱锥
的体积最大时,三棱锥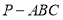 外接球的表面积为
外接球的表面积为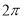 ;
;④若过点P的平面
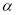 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则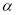 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为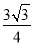
A.1个B.2个C.3个D.4个
相关试题

