【题目】如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 
(1)求证:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的长.
参考答案:
【答案】
(1)证明:∵PG=PD,∴∠PDG=∠PGD,
由于PD为切线,故∠PDA=∠DBA,
又∵∠EGA=∠PGD,∴∠EGA=∠DBA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
从而∠PFA=∠BDA.
又AF⊥EP,∴∠PFA=90°,则∠BDA=90°,
故AB为圆的直径,
∴BD⊥AD.
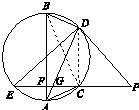
(2)解:连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而得Rt△BDA≌Rt△ACB,
于是∠DAB=∠CBA.
又∵∠DCB=∠DAB,∴∠DCB=∠CBA,故DC∥AB.
∵AB⊥EP,∴DC⊥EP,∠DCE为直角,
∴ED为直径,又由(1)知AB为圆的直径,
∴DE=AB=6
【解析】(1)由已知PG=PD,得到∠PDG=∠PGD,由切割弦定理得到∠PDA=∠DBA,进一步得到∠EGA=∠DBA,从而∠PFA=∠BDA.最后可得∠BDA=90°,说明AB为圆的直径;(2)连接BC,DC.由AB是直径得到∠BDA=∠ACB=90°,然后由Rt△BDA≌Rt△ACB,得到∠DAB=∠CBA.再由∠DCB=∠DAB可推得DC∥AB.进一步得到ED为直径,则ED长可求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件4的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如下表:
752
029
714
985
034
437
863
694
141
469
037
623
804
601
366
959
742
761
428
261
根据以上方法及数据,估计事件A的概率为( )
A.0.384B.0.65C.0.9D.0.904
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心
 为的圆,满足下列条件:圆心
为的圆,满足下列条件:圆心 位于
位于 轴正半轴上,与直线
轴正半轴上,与直线 相切且被轴
相切且被轴 截得的弦长为
截得的弦长为 ,圆
,圆 的面积小于13.
的面积小于13.(Ⅰ)求圆
 的标准方程;
的标准方程;(Ⅱ)设过点
 的直线
的直线 与圆
与圆 交于不同的两点
交于不同的两点 ,以
,以 为邻边作平行四边形
为邻边作平行四边形 .是否存在这样的直线
.是否存在这样的直线 ,使得直线
,使得直线 与
与 恰好平行?如果存在,求出
恰好平行?如果存在,求出 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,证明:
时,证明: 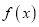 为偶函数;
为偶函数;(2)若
 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(3)若
 ,求实数
,求实数 的取值范围,使
的取值范围,使 在
在 上恒成立.
上恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若函数
,若函数 的图象与
的图象与 轴的交点个数不少于2个,则实数
轴的交点个数不少于2个,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B. 
C.
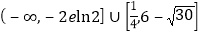 D.
D. 
-
科目: 来源: 题型:
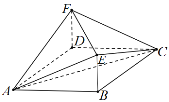
查看答案和解析>>【题目】如图,在多面体
 中,四边形
中,四边形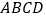 是菱形,
是菱形,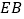 ⊥平面
⊥平面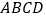 且
且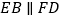 .
.
(1)求证:平面
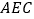 ⊥平面
⊥平面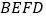 ;
;(2)若
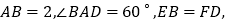 设
设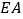 与平面
与平面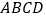 所成夹角为
所成夹角为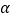 ,且
,且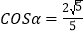 ,求二面角
,求二面角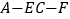 的余弦值.
的余弦值. -
科目: 来源: 题型:
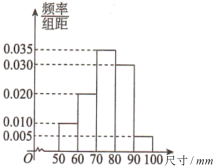
查看答案和解析>>【题目】某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:
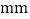 )并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸
)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸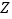 服从正态分布
服从正态分布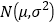 ,其中
,其中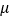 近似为零件样本平均数
近似为零件样本平均数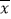 ,
,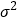 近似为零件样本方差
近似为零件样本方差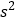 .
.(1)求这批零件样本的
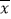 和
和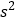 的值(同一组中的数据用该组区间的中点值作代表);
的值(同一组中的数据用该组区间的中点值作代表);(2)假设生产状态正常,求
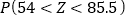 ;
;(3)若从生产线中任取一零件,测量其尺寸为
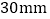 ,根据
,根据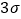 原则判断该生产线是否正常?
原则判断该生产线是否正常?附:
 ;若
;若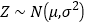 ,则
,则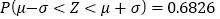 ,
, 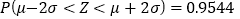 ,
,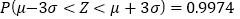 .
.
相关试题

