【题目】已知三棱柱![]() 中,
中, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() .
.
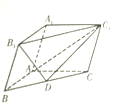
(Ⅰ)求证: ![]() 面
面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成线面角的正弦值.
所成线面角的正弦值.
参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可证得侧面![]() 底面
底面![]() 于
于![]() ,而
,而![]() 在底面
在底面![]() 内,故
内,故![]() 面
面![]() .
.
(Ⅱ)首先做出直线与平面所成的角,然后结合结合关系整理计算即可求得直线![]() 与平面
与平面![]() 所成线面角的正弦值是
所成线面角的正弦值是![]() .
.
试题解析:
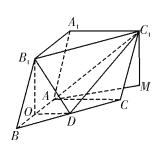
(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
![]() 中,
中, ![]() ,故
,故![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
又![]() ,而
,而![]() 与
与![]() 相交于
相交于![]() ,∴
,∴![]() 面
面![]() ,
,
故![]() ,又
,又![]() ,所以
,所以![]() ,
,
又∵侧面![]() 底面
底面![]() 于
于![]() ,
, ![]() 在底面
在底面![]() 内,∴
内,∴![]() 面
面![]() .
.
(Ⅱ)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
, ![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
由(Ⅰ)知![]() ,侧面
,侧面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]() ,由等边
,由等边![]() 知
知![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,
,
由(Ⅰ)知![]() 面
面![]() ,所以
,所以![]() ,∴四边形
,∴四边形![]() 是正方形,
是正方形,
∵![]() ,∴
,∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
所以直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A
85
80
85
60
90
B
70
x
95
y
75
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,边AB、AD的长分别为2,1,若M,N分别是边BC、CD上的点,且满足
 =
= 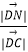 =λ.
=λ. 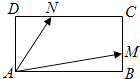
(1)当λ= 时,求向量
时,求向量 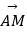 和
和 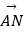 夹角的余弦值;
夹角的余弦值;
(2)求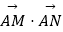 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
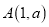 ,圆
,圆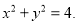
(1)过点
 的圆的切线只有一条,求
的圆的切线只有一条,求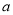 的值及切线方程;
的值及切线方程;(2)若过点
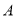 且在两坐标轴上截距相等的直线被圆截得的弦长为
且在两坐标轴上截距相等的直线被圆截得的弦长为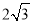 ,求
,求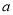 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(α)=
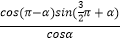 .
.
(1)若α为第二象限角且f(α)=﹣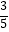 ,求
,求 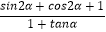 的值;
的值;
(2)若5f(α)=4f(3α+2β).试问tan(2α+β)tan(α+β)是否为定值(其中α≠kπ+ ,α+β≠kπ+
,α+β≠kπ+  ,2α+β≠kπ+
,2α+β≠kπ+  ,3α+2β≠kπ+
,3α+2β≠kπ+  ,k∈Z)?若是,请求出定值;否则,说明理由.
,k∈Z)?若是,请求出定值;否则,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
设函数
 .
.(1)证明:
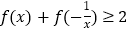 ;
;(2)若不等式
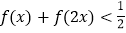 的解集是非空集,求
的解集是非空集,求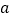 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
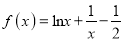 ,
, 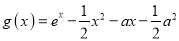 (
(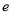 是自然对数的底数,
是自然对数的底数, 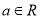 ).
).(Ⅰ)求证:
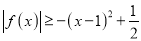 ;
;(Ⅱ)已知
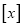 表示不超过
表示不超过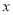 的最大整数,如
的最大整数,如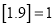 ,
, 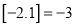 ,若对任意
,若对任意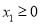 ,都存在
,都存在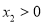 ,使得
,使得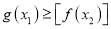 成立,求实数
成立,求实数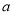 的取值范围.
的取值范围.
相关试题

