
【题目】已知一家公司生产某种品牌服装的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件需另投入
千件需另投入![]() 万元.设该公司一年内共生产该品牌服装
万元.设该公司一年内共生产该品牌服装![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且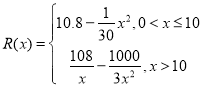 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数![]() 是奇函数;
是奇函数;
②将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图像;
的图像;
③若![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
④![]() 是函数
是函数![]() 的图像的一条对称轴;
的图像的一条对称轴;
⑤函数![]() 的图像关于点
的图像关于点![]() 中心对称。
中心对称。
其中,正确的命题序号是______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦距为
的焦距为![]() ,斜率为
,斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过左焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]()
![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,问:
,问:![]() 是否为定值?若是,求出此定值,若不是,说明理由.
是否为定值?若是,求出此定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的定义域为(-1, 1); ②
的定义域为(-1, 1); ②![]() 的值域为(
的值域为(![]() ,
, ![]() );
);
③![]() 的图象关于原点成中心对称; ④
的图象关于原点成中心对称; ④![]() 在其定义域上是减函数;
在其定义域上是减函数;
⑤对![]() 的定义城中任意
的定义城中任意![]() 都有
都有![]() .
.
其中正确的结论序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为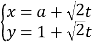 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com