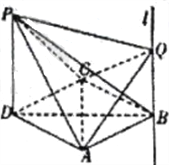
【题目】四棱锥![]() 中,
中,![]() 面
面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,![]() 为直线
为直线![]() 上一动点.
上一动点.
(1)求证:![]() ;
;
(2)当面![]() 面
面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)由![]() 平面
平面![]() 得
得![]() ,又在菱形
,又在菱形![]() 中有
中有![]() ,故得
,故得![]() 平面
平面![]() ,于是得到
,于是得到![]() .(2)结合题意可得
.(2)结合题意可得![]() 平面
平面![]() ,故
,故![]() .根据面
.根据面![]() 面
面![]() 得到
得到![]() ,然后根据几何图形的计算得到
,然后根据几何图形的计算得到![]() ,于是
,于是![]() ,
,![]() ,又
,又![]() ,由此可得所求的三棱锥的体积.
,由此可得所求的三棱锥的体积.
详解:(1)∵![]() ,
,
∴直线![]() 确定一平面
确定一平面![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
由题意知直线![]() 在面
在面![]() 上的射影为
上的射影为![]() ,
,
又在菱形![]() 中有
中有![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由题意得![]() 和
和![]() 都是以
都是以![]() 为底的等腰三角形,设
为底的等腰三角形,设![]() 和
和![]() 的交点为
的交点为![]() ,
,
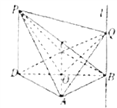
连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
又平面![]() 面
面![]() ,平面
,平面![]()
![]()
![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
∴![]() .
.
在菱形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,设
中,设![]() ,则
,则![]() .
.
∴在![]() 中,
中,![]() ,
,
又在直角梯形![]() 中,
中,![]() ,
,
故![]() ,
,
解得![]() ,即
,即![]() .
.
∴![]() ,
,![]()
∴![]() .
.

