【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在正整数k=10使得
;(3)存在正整数k=10使得![]() 对一切
对一切![]() 恒成立.
恒成立.
【解析】
(1)由题意首先确定数列的前n项和,然后利用前n项和与通项公式的关系求解数列的通项公式即可;
(2)首先裂项求和求得![]() ,然后结合前n项和的范围得到关于m的不等式,求解不等式即可确定实数m的取值范围;
,然后结合前n项和的范围得到关于m的不等式,求解不等式即可确定实数m的取值范围;
(3)解法一:计算![]() 的值,确定
的值,确定![]() 取得最大值时的n的取值即可求得实数k的值;
取得最大值时的n的取值即可求得实数k的值;
解法二:由题意可知,满足题意时有![]() ,据此求解实数k的范围,结合k为正整数即可求得实数k的值.
,据此求解实数k的范围,结合k为正整数即可求得实数k的值.
(1)设数列![]() 的前n项和为
的前n项和为![]() ,
,
由于数列{an}的前n项的“均倒数”为![]() ,
,
所以![]() ,
,
![]() =
=![]() ,
,
当![]() ,
,
当![]() ,
,
![]() (对当
(对当![]() 成立),
成立),
![]() .
.
(2)![]() =
=![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
![]() <
<![]() 对一切
对一切![]() 恒成立,
恒成立,
![]() ,
,
解之得![]() ,
,
即m的取值范围是![]() .
.
(3)解法一:![]() =
=![]() ,
,
由于![]() =
=![]() ,
,
![]() 时
时![]() ,
,![]() 时
时![]() ,
,
![]() 时
时![]() 取得最大值,
取得最大值,
即存在正整数k=10使得![]() 对一切
对一切![]() 恒成立.
恒成立.
解法二:![]() =
=![]() ,
,
假设存在正整数k使得![]() 则
则![]() 为数列
为数列![]() 中的最大项,
中的最大项,
由![]() 得
得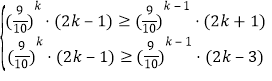 ,
,
![]() ,
,
又![]() ,
,
![]() k=10,
k=10,
即存在正整数k=10使得![]() 对一切
对一切![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 关于直线
关于直线 对称,且圆心在
对称,且圆心在 轴上.
轴上.(1)求
 的标准方程;
的标准方程;(2)已经动点
 在直线
在直线 上,过点
上,过点 引
引 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 .
.①记四边形
 的面积为
的面积为 ,求
,求 的最小值;
的最小值;②证明直线
 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分15分)已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上。
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=an·bn,求数列{cn}的前n项和Tn
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足
 ,乙城市收益Q与投入a(单位:万元)满足
,乙城市收益Q与投入a(单位:万元)满足 ,设甲城市的投入为x(单位:万元),两个城市的总收益为
,设甲城市的投入为x(单位:万元),两个城市的总收益为 (单位:万元).
(单位:万元).(1)求
 及定义域;
及定义域;(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为( )
A.(﹣∞,2)
B.(﹣∞,2]
C.(2,+∞)
D.[2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
相关试题

