【题目】已知函数![]() ,无穷数列
,无穷数列![]() 满足
满足![]() ,
, ![]()
(Ⅰ)若![]() ,求
,求![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列,求
成等比数列,求![]() 的值;
的值;
(Ⅲ)是否存在![]() ,使得
,使得![]() 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的![]() ;若不存在,说明理由.
;若不存在,说明理由.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() .(Ⅲ)当且仅当
.(Ⅲ)当且仅当![]() 时,
时, ![]() ,构成等差数列.
,构成等差数列.
【解析】试题分析:
(Ⅰ)根据递推关系求解即可.(Ⅱ)由条件得![]() ,
, ![]() ,分类讨论去掉绝对值,并根据
,分类讨论去掉绝对值,并根据![]() ,
, ![]() ,
, ![]() 成等比数列可求得
成等比数列可求得![]() 的值.(Ⅲ)由条件得
的值.(Ⅲ)由条件得![]() ,假设存在
,假设存在![]() 满足条件,则
满足条件,则![]() ,即
,即![]() ,经分类讨论去掉绝对值可得当且仅当
,经分类讨论去掉绝对值可得当且仅当![]() 时,
时, ![]() ,构成等差数列.
,构成等差数列.
试题解析:
(Ⅰ)![]() .
.
(Ⅱ)由题意得![]()
![]() .
.
当![]() 时,
时, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 成等比数列,
成等比数列,
∴![]() ,
,
解得![]() .
.
当![]() 时,
时, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 成等比数列
成等比数列
∴![]() ,
,
解得![]() (舍去).
(舍去).
综上可得![]() 或
或![]() .
.
(Ⅲ)假设这样的等差数列存在,那么![]() .
.
由![]() 得
得![]()
![]() .
.
以下分情况讨论:
①当![]() 时,由
时,由![]() 得
得![]() ,与
,与![]() 矛盾;
矛盾;
②当![]() 时,由
时,由![]() 得
得![]() ,①
,①
从而![]() ,所以
,所以![]() 是一个等差数列;
是一个等差数列;
③当![]() 时,则公差
时,则公差![]() ,
,
因此存在![]() 使得
使得![]() .
.
此时![]() ,与
,与![]() 矛盾.
矛盾.
综合①②③可知,当且仅当![]() 时,
时, ![]() 构成等差数列.
构成等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )

A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8
C. 12 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级1 600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图,根据直方图的数据,下列结论错误的是( )
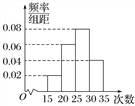
A. 该校九年级学生1分钟仰卧起坐的次数的中位数为26.25
B. 该校九年级学生1分钟仰卧起坐的次数的众数为27.5
C. 该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人
D. 该校九年级学生1分钟仰卧起坐的次数少于20次的约有32人
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一直角边为股,斜边为弦.若a,b,c为直角三角形的三边,其中c为斜边,则a2+b2=c2,称这个定理为勾股定理.现将这一定理推广到立体几何中:在四面体O-ABC中,∠AOB=∠BOC=∠COA=90°,S为顶点O所对面的面积,S1,S2,S3分别为侧面△OAB,△OAC,△OBC的面积,则下列选项中对于S,S1,S2,S3满足的关系描述正确的为( )
A. S2=S+S+S B.
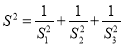
C. S=S1+S2+S3 D.
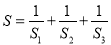
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·武昌调研)如图,在圆内画1条线段,将圆分成2部分;画2条相交线段,将圆分割成4部分;画3条线段,将圆最多分割成7部分;画4条线段,将圆最多分割成11部分.则
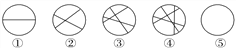
(1)在圆内画5条线段,将圆最多分割成________部分;
(2)在圆内画n条线段,将圆最多分割成________部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次珠宝展览会上,某商家展出一套珠宝首饰,第1件首饰是1颗珠宝,第2件首饰是由6颗珠宝构成的如图1所示的正六边形,第3件首饰是由15颗珠宝构成的如图2所示的正六边形,第4件首饰是由28颗珠宝构成的如图3所示的正六边形,第5件首饰是由45颗珠宝构成的如图4所示的正六边形,以后每件首饰都在前一件的基础上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断:
(1)第6件首饰上应有________颗珠宝;
(2)前n(n∈N*)件首饰所用珠宝总颗数为________.(结果用n表示)
相关试题

