搜索
【题目】某公司今年一月份推出新产品A，其成本价为492元/件，经试销调查，销售量与销售价的关系如下表：
销售价（x/元件） | 650 | 662 | 720 | 800 |
销售量（y件） | 350 | 333 | 281 | 200 |
由此可知，销售量y（件）与销售价x（元/件）可近似看作一次函数y=kx+b的关系（通常取表中相距较远的两组数据所得一次函数较为精确）．
（1）写出以x为自变量的函数y的解析式及定义域；
（2）试问：销售价定为多少时，一月份销售利润最大？并求最大销售利润和此时的销售量．
参考答案：
【答案】
（1）解：由题意知 
，
解得k=﹣1，b=1000，∴y=﹣x+1000
由于y为非负整数，所以0≤x≤1000
（2）解：设一月份的利润为S元，由题意得S=（x﹣492）（1000﹣x）=﹣（x﹣746）2+64516
∴当x=746元/件时，一月份销售收入 最大为64516元
【解析】（1）利用已知的函数关系式，代入数据求解即可．（2）推出利润的函数的解析式，利用二次函数的性质求解即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】[选修4-5：不等式选讲]
已知函数f（x）=|2x﹣1|+|x+1|，g（x）=|x﹣a|+|x+a|．
（Ⅰ）解不等式f（x）＞9；
（Ⅱ）x1∈R，x2∈R，使得f（x1）=g（x2），求实数a的取值范围。
-
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）是定义在（﹣1，+∞）内的增函数，且f（xy）=f（x）+f（y）若f（3）=1且f（a）＞f（a﹣1）+2
求：
（1）f（9）的值，
（2）求a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°，距离为12
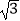海里；在A处看灯塔C在货轮的北偏西30°，距离为8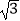海里；货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°．（要画图）
（1）A处与D处之间的距离；
（2）灯塔C与D处之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】下表是一位母亲给儿子作的成长记录：
年龄/周岁
3
4
5
6
7
8
9
身高/cm
94.8
104.2
108.7
117.8
124.3
130.8
139.1
根据以上样本数据，她建立了身高
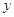（cm）与年龄x（周岁）的线性回归方程为 
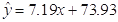，给出下列结论：
①y与x具有正的线性相关关系；
②回归直线过样本的中心点（42，117.1）；
③儿子10岁时的身高是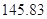
cm；
④儿子年龄增加1周岁，身高约增加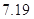
cm.
其中，正确结论的个数是
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列四个结论,其中正确的个数为（ ）. ①已
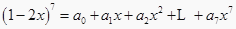，则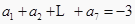 
②过原点作曲线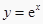
的切线,则切线方程为 
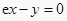（其中e为自然对数的底数）；
③已知随机变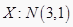
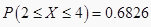，则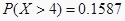 
④已知n为正偶数,用数学归纳法证明等式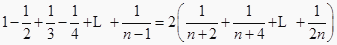
时,若假设 
时,命题为真,则还需利用归纳假设再证明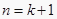 
时等式成立,即可证明等式对一切正偶数n都成立.
⑤在回归分析中,常用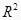
来刻画回归效果,在线性回归模型中， 
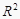表示解释变量对于预报变量变化的贡献率 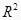越接近1,表示回归的效果越好.
A.2
B.3
C.4
D.5 -
科目： 来源： 题型：
查看答案和解析>>【题目】证明f（x）=﹣x2+3在（0，+∞）上是减函数．
相关试题
