【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2sin Acos B=2sin C﹣sin B. ①求角A;
②若a=4 ![]() ,b+c=8,求△ABC 的面积.
,b+c=8,求△ABC 的面积.
参考答案:
【答案】解:①∵2sinAcosB=2sinC﹣sinB, ∵由正弦定理可得:2acosB=2c﹣b,即:cosB= ![]() ,
,
又∵cosB= ![]() ,
,
∴ ![]() =
= ![]() ,解得:b2+c2﹣a2=bc,
,解得:b2+c2﹣a2=bc,
∴cosA= ![]() =
= ![]() =
= ![]() ,
,
又∵A∈(0,π),
∴A= ![]()
②∵由余弦定理可得:a2=b2+c2﹣2bccosA,a=4 ![]() ,b+c=8,
,b+c=8,
∴(4 ![]() )2=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,
)2=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,
∴bc= ![]() ,
,
∴△ABC 的面积S= ![]() bcsinA=
bcsinA= ![]() =
= ![]()
【解析】①由正弦定理化简已知等式可得cosB= ![]() ,结合余弦定理可求b2+c2﹣a2=bc,可求cosA,结合范围A∈(0,π),可求A的值.②由已知及余弦定理可得bc=
,结合余弦定理可求b2+c2﹣a2=bc,可求cosA,结合范围A∈(0,π),可求A的值.②由已知及余弦定理可得bc= ![]() ,进而利用三角形面积公式即可计算得解.
,进而利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在区间(0,+∞)内的单调函数,且对x∈(0,∞),都有f[f(x)﹣lnx]=e+1,设f′(x)为f(x)的导函数,则函数g(x)=f(x)﹣f′(x)的零点个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二项式
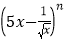 展开式中各项系数之和比各二项式系数之和大240,
展开式中各项系数之和比各二项式系数之和大240,(1)求
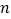 ;(2)求展开式中含
;(2)求展开式中含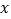 项的系数;(3)求展开式中所有含
项的系数;(3)求展开式中所有含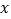 的有理项.
的有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)的表达式为f(x)=
 (c≠0),则函数f(x)的图象的对称中心为(﹣
(c≠0),则函数f(x)的图象的对称中心为(﹣  ,
,  ),现已知函数f(x)=
),现已知函数f(x)=  ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f(  )(n∈N),则此数列前2017项的和为 .
)(n∈N),则此数列前2017项的和为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】
 是定义在R上的函数,对
是定义在R上的函数,对 ∈R都有
∈R都有 ,且当
,且当 >0时,
>0时, <0,且
<0,且 =1.
=1.(1)求
 的值;
的值;(2)求证:
 为奇函数;
为奇函数;(3)求
 在[-2,4]上的最值.
在[-2,4]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入
 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?(用数字作答)
(1)甲不能跑第一棒和第四棒;(2)甲不能跑第一棒,乙不能跑第四棒
相关试题

