【题目】若函数f(x)的表达式为f(x)= ![]() (c≠0),则函数f(x)的图象的对称中心为(﹣
(c≠0),则函数f(x)的图象的对称中心为(﹣ ![]() ,
, ![]() ),现已知函数f(x)=
),现已知函数f(x)= ![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f( ![]() )(n∈N),则此数列前2017项的和为 .
)(n∈N),则此数列前2017项的和为 .
参考答案:
【答案】-2016
【解析】解:若函数f(x)的表达式为f(x)= ![]() (c≠0), 则函数f(x)的图象的对称中心为(﹣
(c≠0), 则函数f(x)的图象的对称中心为(﹣ ![]() ,
, ![]() ),
),
现已知函数f(x)= ![]() ,则对称中心为(
,则对称中心为( ![]() ,﹣1),
,﹣1),
即有f(x)+f(1﹣x)=﹣2,
则数列前2017项的和为S2017=f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1),
)+f(1),
则S2017=f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1),
)+f(1),
相加可得2S2017=[f( ![]() )+f(
)+f( ![]() )]+[f(
)]+[f( ![]() )+f(
)+f( ![]() )]+…+2f(1)
)]+…+2f(1)
=﹣2+(﹣2)+…+(﹣2)+0=﹣2×2016,
则此数列前2017项的和为﹣2016.
故答案为:﹣2016.
由已知结论可得f(x)的对称中心为( ![]() ,﹣1),即有f(x)+f(1﹣x)=﹣2,此数列前2017项的和按正常顺序写一遍,再倒过来写,即运用数列的求和方法:倒序球和法,化简即可得到所求和.
,﹣1),即有f(x)+f(1﹣x)=﹣2,此数列前2017项的和按正常顺序写一遍,再倒过来写,即运用数列的求和方法:倒序球和法,化简即可得到所求和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)排成前后两排,前排3人,后排4人;(2)全体站成一排,甲不站排头也不站排尾;
(3)全体站成一排,女生必须站在一起;(4)全体站成一排,男生互不相邻.(用数字作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在区间(0,+∞)内的单调函数,且对x∈(0,∞),都有f[f(x)﹣lnx]=e+1,设f′(x)为f(x)的导函数,则函数g(x)=f(x)﹣f′(x)的零点个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二项式
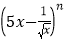 展开式中各项系数之和比各二项式系数之和大240,
展开式中各项系数之和比各二项式系数之和大240,(1)求
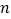 ;(2)求展开式中含
;(2)求展开式中含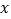 项的系数;(3)求展开式中所有含
项的系数;(3)求展开式中所有含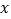 的有理项.
的有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A,B,C所对的边分别为a,b,c,且2sin Acos B=2sin C﹣sin B. ①求角A;
②若a=4 ,b+c=8,求△ABC 的面积.
,b+c=8,求△ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 是定义在R上的函数,对
是定义在R上的函数,对 ∈R都有
∈R都有 ,且当
,且当 >0时,
>0时, <0,且
<0,且 =1.
=1.(1)求
 的值;
的值;(2)求证:
 为奇函数;
为奇函数;(3)求
 在[-2,4]上的最值.
在[-2,4]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入
 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
相关试题

