【题目】已知椭圆E: ![]() =1(a>b>0)上任意一点到两焦点距离之和为
=1(a>b>0)上任意一点到两焦点距离之和为 ![]() ,离心率为
,离心率为 ![]() ,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
,左、右焦点分别为F1 , F2 , 点P是右准线上任意一点,过F2作直线PF2的垂线F2Q交椭圆于Q点.
(1)求椭圆E的标准方程;
(2)证明:直线PQ与直线OQ的斜率之积是定值;
(3)证明:直线PQ与椭圆E只有一个公共点.
参考答案:
【答案】
(1)解:由题意可得 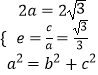 ,解得
,解得 ![]() ,c=1,
,c=1, ![]()
所以椭圆E: ![]() .
.
(2)解:由(1)可知:椭圆的右准线方程为 ![]() ,
,
设P(3,y0),Q(x1,y1),
因为PF2⊥F2Q,所以 ![]() ,
,
所以﹣y1y0=2(x1﹣1)
又因为 ![]() 且
且 ![]() 代入化简得
代入化简得 ![]() .
.
即直线PQ与直线OQ的斜率之积是定值 ![]()
(3)解:由(2)知, ![]() ,
, ![]() ,
,
∴ ![]() .
.
∴直线PQ的方程为 ![]() ,即
,即 ![]() ,
,
联立 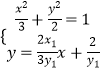 得
得 ![]() ,
,
∵ ![]() ,
, ![]() .
.
∴化简得: ![]() ,又△=0,
,又△=0,
解得x=x1,所以直线PQ与椭圆C相切,只有一个交点
【解析】(1)由题意可得 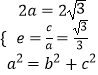 ,解出即可;(2)由(1)可知:椭圆的右准线方程为
,解出即可;(2)由(1)可知:椭圆的右准线方程为 ![]() ,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得
,设P(3,y0),Q(x1 , y1),由PF2⊥F2Q,可得 ![]() ,利用斜率计算公式可得kPQkOQ及
,利用斜率计算公式可得kPQkOQ及 ![]() 代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为
代入化简得直线PQ与直线OQ的斜率之积是定值.(3)由(2)知,直线PQ的方程为 ![]() ,即
,即 ![]() ,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
,与椭圆的方程联立,消去一个未知数得到关于x的一元二次方程,只要证明△=0即可.
【考点精析】关于本题考查的直线的斜率和椭圆的标准方程,需要了解一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥
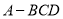 中,
中, 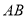 垂直于平面
垂直于平面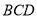 ,
, 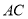 垂直于
垂直于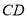 ,且
,且 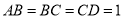 ,则三棱锥
,则三棱锥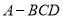 的外接球的球面面积为__________.
的外接球的球面面积为__________.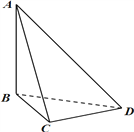
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|3≤3x≤27},
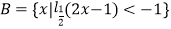 .
.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】请认真阅读下列程序框图,然后回答问题,其中n0∈N.
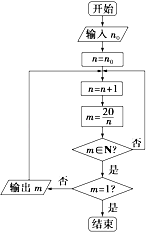
(1)若输入n0=0,写出所输出的结果;
(2)若输出的结果中有5,求输入的自然数n0的所有可能的值;
(3)若输出的结果中,只有三个自然数,求输入的自然数n0的所有可能的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
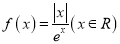 ,若关于
,若关于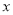 的方程
的方程 恰好有 4 个不相等的实数解,则实数
恰好有 4 个不相等的实数解,则实数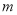 的取值范围为( )
的取值范围为( )A.
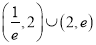 B.
B.  C.
C. 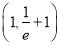 D.
D. 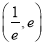
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照
 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.(1)求直方图的
 的值;
的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若
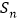 是公差不为0的等差数列
是公差不为0的等差数列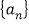 的前
的前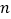 项和,且
项和,且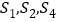 成等比数列,
成等比数列,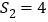 .
.(1)求数列
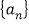 的通项公式;
的通项公式;(2)设
 是数列
是数列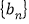 的前
的前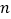 项和,求使得
项和,求使得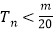 对所有
对所有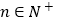 都成立的最小正整数
都成立的最小正整数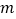 .
.
相关试题

