【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
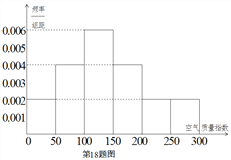
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析: (Ⅰ)根据频率分布直方图知小长方形面积为对应区间概率,先计算空气质量优良区间对应的概率,再根据频数等于总数乘以概率得空气质量优良的天数,(Ⅱ)先确定随机变量取法,再分别求对应概率,列表得分布列,最后根据期望公式求数学期望.
试题解析: (Ⅰ)由直方图可估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数为
天计算)全年空气质量优良的天数为
![]() (天).
(天).
(Ⅱ)由题可知, ![]() 的所有可能取值为:
的所有可能取值为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则: ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 在区间
在区间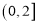 上单调递增;
上单调递增;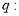 函数
函数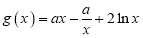 在其定义域上存在极值.
在其定义域上存在极值.(1)若
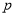 为真命题,求实数
为真命题,求实数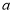 的取值范围;
的取值范围;(2)如果“
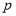 或
或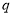 ”为真命题,“
”为真命题,“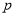 且
且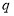 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x
[11,13)
[13,15)
[15,17)
[17,19)
[19,21)
[21,23)
频数
2
12
34
38
10
4
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的中心在原点,一个焦点为
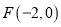 ,且长轴与短轴长的比是
,且长轴与短轴长的比是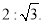
(1)求椭圆C的方程;
(2)设点
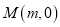 在 椭圆C的长轴上,点P是椭圆上任意一点,当
在 椭圆C的长轴上,点P是椭圆上任意一点,当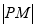 最小时,点P恰好落在椭圆的右顶点上,求实数
最小时,点P恰好落在椭圆的右顶点上,求实数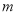 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
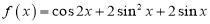 .
.(1)将函数
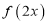 的图像向右平移
的图像向右平移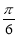 个单位得到函数
个单位得到函数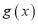 的图像,若
的图像,若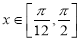 ,求函数
,求函数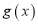 的值域;
的值域;(2)已知
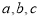 ,分别为
,分别为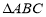 中角
中角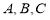 的对边,且满足
的对边,且满足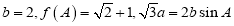 ,求
,求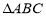 的面积.
的面积. -
科目: 来源: 题型:
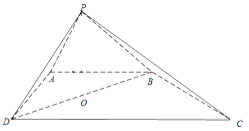
查看答案和解析>>【题目】如图,四棱锥
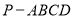 的底面是直角梯形,
的底面是直角梯形, ,
,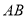 ⊥
⊥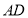 ,△
,△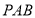 和△
和△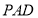 是两个边长为2的正三角形,
是两个边长为2的正三角形,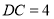 .
.
(1)求证:平面
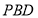 ⊥平面
⊥平面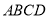 ;
;(2)求二面角
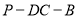 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P—ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形,
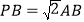 ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.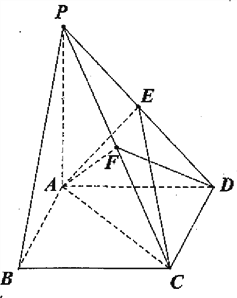
相关试题

