【题目】如图,已知长方形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点. 将
的中点. 将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
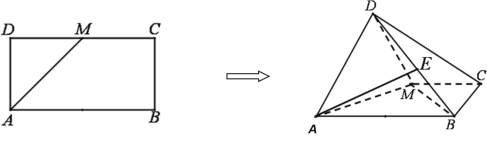
(1)求证:![]() .
.
(2)点![]() 是线段
是线段![]() 上的一动点,当二面角
上的一动点,当二面角![]() 大小为
大小为![]() 时,试确定点
时,试确定点![]() 的位置.
的位置.
参考答案:
【答案】(1)见解析;(2)当E位于线段DB之间,且 ![]()
【解析】
(1)取AM的中点O,AB的中点N,则![]() 两两垂直,以O为原点建立如图所示的空间直角坐标系, 写出坐标,证明
两两垂直,以O为原点建立如图所示的空间直角坐标系, 写出坐标,证明![]() 即可;
即可;
(2)根据![]() ,设出点E的坐标,利用平面法向量的数量积求解出
,设出点E的坐标,利用平面法向量的数量积求解出![]() ,进而得出比值,得到结论。
,进而得出比值,得到结论。
解:取AM的中点O,AB的中点N,则![]() 两两垂直,
两两垂直,
以O为原点建立如图所示的空间直角坐标系,
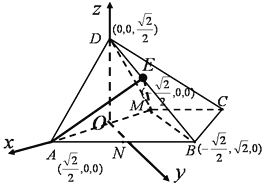
如图,根据已知条件,得![]() ,
,![]() ,
,![]() ,
,![]()
(1)由于![]()
则![]() ,故
,故![]() .
.
(2)设存在满足条件的点E,并设![]() ,
,
则![]()
则点E的坐标为![]() .(其中
.(其中![]() )
)
易得平面ADM的法向量可以取![]() ,
,
设平面AME的法向量为![]() ,
,
则![]() ,
, ![]()
则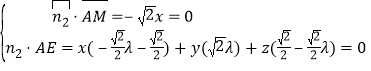
解得![]() ,取
,取![]()
由于二面角![]() 大小为
大小为![]() ,
,
则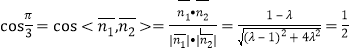 ,
,
由于![]() ,故解得
,故解得![]() .
.
故当E位于线段DB之间,且![]() 时,二面角
时,二面角![]() 大小为
大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,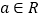 .
.(Ⅰ)当
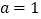 时,求
时,求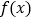 的图象在点
的图象在点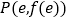 处的切线方程;
处的切线方程;(Ⅱ)设函数
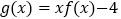 ,讨论函数
,讨论函数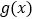 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”. 执行该程序框图,若输入的
 分别为16,20,则输出的
分别为16,20,则输出的 ( )
( )
A. 0B. 2C. 4D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A.一条直线与两个平行平面中的一个平行,则必与另一个平面平行
B.空间中两条直线要么平行,要么相交
C.空间中任意的三个点都能唯一确定一个平面
D.对于空间中任意两条直线,总存在平面与这两条直线都平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
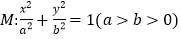 的离心率是
的离心率是 ,上顶点B是抛物线
,上顶点B是抛物线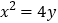 的焦点.
的焦点.(1)求椭圆
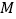 的标准方程;
的标准方程;(2)若
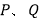 是椭圆
是椭圆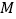 上的两个动点,且
上的两个动点,且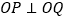 (
( 是坐标原点),试问:点到直线的距离是否为定值?若是,试求出这个定值;若不是,请说明理由.
是坐标原点),试问:点到直线的距离是否为定值?若是,试求出这个定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABSCD中,四边形ABCD为矩形,AB=1,△BSC为边长为2的正三角形,将△BSC沿BC折起,使得侧面SAD垂直于平面ABCD,E、F分别为SA、DC的中点.
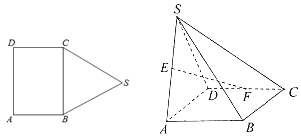
(1)求证:EF∥面SBC;
(2)求四棱锥S﹣ABCD的侧面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
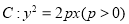 的焦点为
的焦点为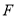 ,其上一点
,其上一点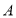 在准线上的射影为
在准线上的射影为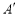 ,△
,△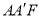 恰为一个边长为4的等边三角形.
恰为一个边长为4的等边三角形.(1)求抛物线
 的方程;
的方程;(2)若过定点
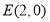 的直线
的直线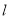 交抛物线
交抛物线 于
于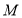 ,
,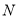 两点,
两点,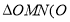 为坐标原点)的面积为
为坐标原点)的面积为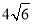 ,求直线
,求直线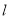 的方程.
的方程.
相关试题

