【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:

(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
(2)若对年龄在![]() 的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

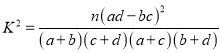
参考答案:
【答案】(1)没有99%的把握(2)![]()
【解析】试题分析:(1)由频率分布表中的数据得到a,b,c,d的值,然后计算出![]() 的值,由于
的值,由于![]() ,于是得到没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
,于是得到没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
(2)年龄在![]() 中支持“生育二胎”的4人分别为
中支持“生育二胎”的4人分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,不支持“生育二胎”的人记为
,不支持“生育二胎”的人记为![]() ,列出从这5人中随机选出2人的所有的可能的结果,找到“恰好这两人都支持“生育二胎””的所有结果,然后求出概率即可.
,列出从这5人中随机选出2人的所有的可能的结果,找到“恰好这两人都支持“生育二胎””的所有结果,然后求出概率即可.
试题解析:
(1)![]() 列联表为
列联表为
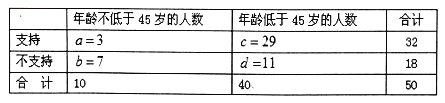
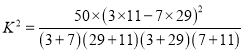
![]()
所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
(2)设年龄在![]() 中支持“生育二胎”的4人分别为
中支持“生育二胎”的4人分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,不支持“生育二胎”的人记为
,不支持“生育二胎”的人记为![]() ,
,
则从年龄在![]() 的被调查人中随机选取两人所有可能的结果有:
的被调查人中随机选取两人所有可能的结果有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
设“恰好这两人都支持“生育二胎””为事件![]() ,
,
则事件![]() 所有可能的结果有:
所有可能的结果有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
所以对年龄在![]() 的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为
的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】潮州统计局就某地居民的月收入调查了
 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在
 )。
)。
(1)求居民月收入在
 的频率;
的频率;(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这
 人中分层抽样方法抽出
人中分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①分类变量
 与
与 的随机变量
的随机变量 越大,说明“
越大,说明“ 与
与 有关系”的可信度越大.
有关系”的可信度越大.②以模型
 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设 ,将其变换后得到线性方程
,将其变换后得到线性方程 ,则
,则 的值分别是
的值分别是 和0.3.
和0.3.③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
 中,
中,  ,
,则
 .正确的个数是( )
.正确的个数是( )A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过定点P(-2,1)作直线l分别与x、y轴交于A、B两点,
(1)求经过点P且在两坐标轴上的截距相等的直线l方程.
(2)求使
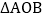 面积为4时的直线l方程。
面积为4时的直线l方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
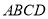 的对角线交于点
的对角线交于点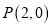 ,边
,边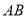 所在直线的方程为
所在直线的方程为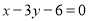 ,点
,点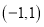 在边
在边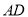 所在的直线上.
所在的直线上.(1)求矩形
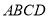 的外接圆的方程;
的外接圆的方程;(2)已知直线
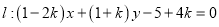 (
(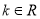 ),求证:直线
),求证:直线 与矩形
与矩形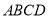 的外接圆恒相交,并求出相交的弦长最短时的直线
的外接圆恒相交,并求出相交的弦长最短时的直线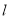 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
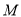 的圆心
的圆心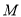 在
在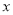 轴上,半径为1,直线
轴上,半径为1,直线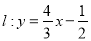 被圆
被圆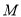 所截的弦长为
所截的弦长为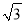 ,且圆心
,且圆心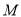 在直线
在直线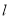 的下方.
的下方.(1)求圆
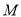 的方程;
的方程;(2)设
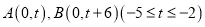 ,若圆
,若圆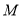 是
是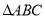 的内切圆,求
的内切圆,求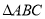 的面积
的面积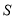 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
已知函数
 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为 .
.(1)求
 的值及函数
的值及函数 的极值;
的极值;(2)证明:当
 时,
时,
(3)证明:对任意给定的正数
 ,总存在
,总存在 ,使得当
,使得当 时,恒有
时,恒有
相关试题

