【题目】已知![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(2)当![]() 时,若
时,若![]() ,都有
,都有![]() 成立,求实数
成立,求实数
![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用![]() 是函数
是函数![]() 的极值点,求出
的极值点,求出![]() ,即可求出
,即可求出![]() 的值;(2)对
的值;(2)对![]() 进行配方,讨论其最值问题,根据题意
进行配方,讨论其最值问题,根据题意![]() ,总有
,总有![]() 成立,只要要求
成立,只要要求![]() ,即可,从而求出
,即可,从而求出![]() 的范围.
的范围.
试题解析:(1)![]() ,又因为
,又因为![]() 是极值点,则
是极值点,则![]() ,则
,则![]() ,经检验,当
,经检验,当![]() 时,
时, ![]() 是
是![]() 极值点,故名满足题意.
极值点,故名满足题意.
(2)当a=2时,f(x)=2x-![]() -5ln x,
-5ln x,
f ′(x)=![]() ,
,
∴当x∈(0, ![]() )时,f ′ (x)>0,f(x)单调递增;
)时,f ′ (x)>0,f(x)单调递增;
当x∈(![]() ,1)时,f ′(x)<0,f(x)单调递减.
,1)时,f ′(x)<0,f(x)单调递减.
∴在(0,1)上,f(x)max=f(![]() )=-3+5ln2.
)=-3+5ln2.
又“x1∈(0,1),x2∈[1,2],都有f(x1)≥g(/span>x2)成立”等价于“f(x)在(0,1)上的最大值不小于g(x)在[1,2]上的最大值”,而g(x)在[1,2]上的最大值为max{g(1),g(2)},
∴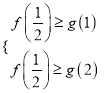 ,即
,即![]() ,
,
解得m≥8-5ln 2.
∴实数m的取值范围是[8-5ln 2,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 ,求
,求 在
在 处的切线方程;
处的切线方程;(2)若
 在区间
在区间 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程。
在平面直角坐标系
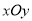 中,已知曲线
中,已知曲线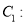
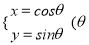 ,以平面直角坐标系
,以平面直角坐标系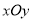 的原点
的原点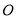 为极点,
为极点, 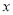 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线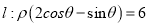 .
.(1)将曲线
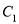 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的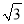 、2倍后得到曲线
、2倍后得到曲线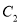
试写出直线
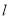 的直角坐标方程和曲线
的直角坐标方程和曲线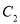 的参数方程;
的参数方程;(2)在曲线
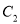 上求一点
上求一点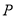 ,使点
,使点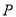 到直线
到直线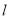 的距离最大,并求出此最大值.
的距离最大,并求出此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}满足:a1=1,an+1=3an , n∈N* . 设Sn为数列{bn}的前n项和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an , 求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一年级的A,B,C三个班共有学生120人,为调查他们的体育锻炼情况,用分层抽样的方法从这三个班中分别抽取4,5,6名学生进行调查. (Ⅰ)求A,B,C三个班各有学生多少人;
(Ⅱ)记从C班抽取学生的编号依次为C1 , C2 , C3 , C4 , C5 , C6 , 现从这6名学生中随机抽取2名做进一步的数据分析.
(i)列出所有可能抽取的结果;
(ii)设A为事件“编号为C1和C2的2名学生中恰有一人被抽到”,求事件A发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令
 .
.
(Ⅰ)证明:数列{bn}是等差数列;
(Ⅱ)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,﹣2),椭圆E:
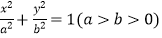 的离心率为
的离心率为 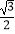 ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为 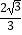 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆E的方程;
(2)设过点A的动直线与椭圆E相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
相关试题

