【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
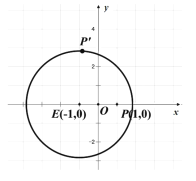
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)折痕为![]() 的垂直平分线,则
的垂直平分线,则![]() ,推导出
,推导出![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,且且
为焦点的椭圆,且且![]() ,
,![]() ,由此能求出的轨迹
,由此能求出的轨迹![]() 的方程.
的方程.
(2)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,,从而
相切,,从而![]() ,由
,由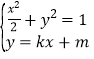 ,得
,得![]() ,由此利用根的判别式、韦达定理、向量的数量积、弦长公式、三角形面积公式,能求出
,由此利用根的判别式、韦达定理、向量的数量积、弦长公式、三角形面积公式,能求出![]() 的面积的取值范围.
的面积的取值范围.
试题解析:
(1)折痕为![]() 的垂直平分线,则
的垂直平分线,则![]() ,由题意知圆
,由题意知圆![]() 的半径为
的半径为![]() ,
,
∴![]() ,
,
∴![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,则
相切,则![]() 到
到![]() 即直线
即直线![]() 的距离:
的距离:
![]() ,即
,即![]() ,
,
由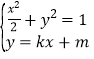 ,消去
,消去![]() ,得
,得![]() ,
,
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]()
![]()
![]()
设![]() ,则
,则![]() ,∴
,∴![]()
![]() ,
,![]() ,
,
∵![]() 关于
关于![]() 在
在![]() 单调递增,∴
单调递增,∴![]() ,∴
,∴![]() 的面积的取值范围是
的面积的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1:x2+y2-2mx-4my+5m2-4=0(m∈R),圆C2:x2+y2=1.
(1)过定点M(1,-2)作圆C2的切线,求切线的方程;
(2)若圆C1与圆C2相交,求m的取值范围;
(3)已知点P(2,0),圆C1上一点A,圆C2上一点B,求|
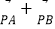 |的最小值的取值范围.
|的最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
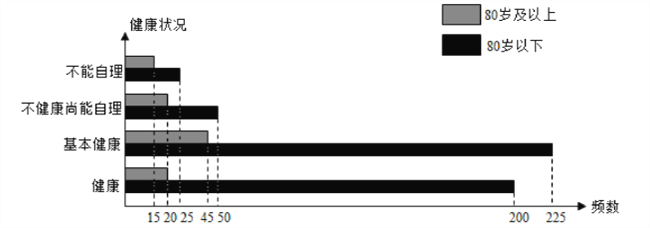
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.
利用样本估计总体,试估计政府执行此计划的年度预算.(单位:亿元,结果保留两位小数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】总体由编号为01,02,03,
 ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )78 16 65 72 08 02 63 14 07 02 43 69 69 38 74
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01
A. 05 B. 09 C. 07 D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 处有一港口,两艘海轮
处有一港口,两艘海轮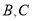 同时从港口
同时从港口 处出发向正北方向匀速航行,海轮
处出发向正北方向匀速航行,海轮 的航行速度为20海里/小时,海轮
的航行速度为20海里/小时,海轮 的航行速度大于海轮
的航行速度大于海轮 .在港口
.在港口 北偏东60°方向上的
北偏东60°方向上的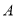 处有一观测站,1小时后在
处有一观测站,1小时后在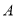 处测得与海轮
处测得与海轮 的距离为30海里,且
的距离为30海里,且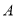 处对两艘海轮
处对两艘海轮 ,
, 的视角为30°.
的视角为30°.
(1)求观测站
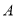 到港口
到港口 的距离;
的距离;(2)求海轮
 的航行速度.
的航行速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
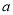 为正的常数,函数
为正的常数,函数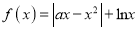 .
.(1)若
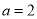 ,求函数
,求函数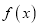 的单调递增区间;
的单调递增区间;(2)设
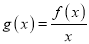 ,求
,求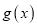 在区间
在区间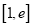 上的最小值.(
上的最小值.(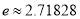 为自然对数的底数)
为自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关命题的说法错误的是( )
A. 若“
 ”为假命题,则p,q均为假命题
”为假命题,则p,q均为假命题B. “
 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. “
 ”的必要不充分条件是“
”的必要不充分条件是“ ”
”D. 若命题p:
 ,
, ,则命题
,则命题 :
: ,
,
相关试题

