【题目】设函数![]() 的反函数为
的反函数为![]() ,若存在函数
,若存在函数![]() 使得对函数
使得对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为函数
为函数![]() 的“Inverse”函数.
的“Inverse”函数.
(1)判断下列哪个函数是函数![]() 的“Inverse”函数并说明理由.
的“Inverse”函数并说明理由.
①![]() ;②
;②![]() ;
;
(2)设函数![]() 存在反函数
存在反函数![]() ,证明函数
,证明函数![]() 存在唯一的“Inverse”函数的充要条件是函数
存在唯一的“Inverse”函数的充要条件是函数![]() 的值域为
的值域为![]() ;
;
(3)设函数![]() 存在反函数
存在反函数![]() ,函数
,函数![]() 为
为![]() 的一个“Inverse”函数,记
的一个“Inverse”函数,记![]() ,其中
,其中![]() ,若对函数
,若对函数![]() 定义域内的任意
定义域内的任意![]() 都有
都有![]() ,求所有满足条件的函数
,求所有满足条件的函数![]() 的解析式.
的解析式.
参考答案:
【答案】(1)②是函数f(x)=log2x的“Inverse”函数,理由见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)分别判断①和②是否满足![]() 即可得到结果;
即可得到结果;
(2)先证充分性,若函数![]() 的值域为
的值域为![]() ,设其定义域为D,则函数
,设其定义域为D,则函数![]() 的定义域为
的定义域为![]() ,值域为D, 令
,值域为D, 令![]() ,
,![]() ,判断是否满足
,判断是否满足![]() ,证明其存在性,再设函数
,证明其存在性,再设函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,利用反证法证明唯一性;再证必要性,若函数
的“Inverse”函数且不相同,利用反证法证明唯一性;再证必要性,若函数![]() 存在唯一的“Inverse”函数,同样利用反证法,假设函数
存在唯一的“Inverse”函数,同样利用反证法,假设函数![]() 的值域为
的值域为![]() ,令
,令 ,
, ,通过证明函数
,通过证明函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,这与唯一性矛盾,从而得证;
的“Inverse”函数且不相同,这与唯一性矛盾,从而得证;
(3)由(2)知,![]() 是
是![]() 的一个“Inverse”函数,易得,
的一个“Inverse”函数,易得,![]() ,即
,即![]() ,根据一一对应的性质可得
,根据一一对应的性质可得![]() ,所以
,所以![]() .
.
(1)易得![]() ,对于①,
,对于①,![]() ,故①不是,
,故①不是,
对于②,![]() ,故②是函数
,故②是函数![]() 的“Inverse”函数;
的“Inverse”函数;
(2)先证充分性,若函数![]() 的值域为
的值域为![]() ,设其定义域为D,
,设其定义域为D,
则函数![]() 的定义域为
的定义域为![]() ,值域为D,
,值域为D,
令![]() ,
,![]() ,
,
则对任意![]() 都有,
都有,![]() ,
,
故函数![]() 为函数
为函数![]() 的“Inverse”函数,存在性得证;
的“Inverse”函数,存在性得证;
设函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,
的“Inverse”函数且不相同,
则存在![]() ,
,![]() ,
,![]() ,且
,且![]() ,因为
,因为![]() 的值域为
的值域为![]() ,
,
故存在![]() ,使得
,使得![]() ,即
,即![]() ,
,![]() ,
,
则![]() ,矛盾,故唯一性得证.
,矛盾,故唯一性得证.
所以函数![]() 存在唯一的“Inverse”函数.
存在唯一的“Inverse”函数.
再证必要性,若函数![]() 存在唯一的“Inverse”函数,
存在唯一的“Inverse”函数,
即存在唯一的函数![]() 满足
满足![]() ,下面用反证法证明必要性.
,下面用反证法证明必要性.
假设函数![]() 的值域为
的值域为![]() ,
,
令 ,
, ,
,
则对任意![]() 都有,
都有,![]() ,
,
且![]() ,
,![]() ,
,
函数![]() 和
和![]() 都为函数
都为函数![]() 的“Inverse”函数且不相同,这与唯一性矛盾,
的“Inverse”函数且不相同,这与唯一性矛盾,
所以函数![]() 的值域为
的值域为![]() ,必要性得证.
,必要性得证.
综上,函数![]() 存在唯一的“Inverse”函数的充要条件是函数
存在唯一的“Inverse”函数的充要条件是函数![]() 的值域为
的值域为![]() ;
;
(3)由(2)知,![]() 是
是![]() 的一个“Inverse”函数,
的一个“Inverse”函数,
由反函数的性质可知,![]() 和
和![]() 都是一一对应的.
都是一一对应的.
则![]() ,
,
又![]() ,则
,则![]() ,
,
即![]() ,根据一一对应的性质可得
,根据一一对应的性质可得![]() ,
,
则![]() ,所以满足条件的函数
,所以满足条件的函数![]() 的解析式为
的解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数
 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
0




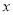



0
2
0
0
(1)请将上表数据补充完整,填写在相应位置,并求出函数
 的解析式;
的解析式;(2)把
 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,求
的图象,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“秃发”是一种常见的毛发疾病,随着发病人群年龄结构的年变化,逐渐引起了社会的广泛关注.一个人出生时头发数量约为100000根,数学徐老师建立了“秃发”函数模型作预估:一个人
 岁时的头发根数为
岁时的头发根数为 ,其中
,其中 称为“脱发指数”.
称为“脱发指数”.(1)杜老师5岁时有74375根头发,请依据模型求出杜老师的“脱发指数”
 的值;
的值;(2)徐老师的学生认为“秃发”函数模型中有两个缺点:①头发的根数应该为整数;②头发的根数不能为负数,徐老师感觉很有道理,将模型作了两处修正,请写出修正后(1)问中杜老师的“秃发”函数模型,并求出杜老师几岁时头发最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 (实数
(实数 为常数)
为常数)(1)当
 时,证明
时,证明 在
在 上单调递减;
上单调递减;(2)若
 ,且
,且 为偶函数,求实数
为偶函数,求实数 的值;
的值;(3)小金同学在求解函数
 的对称中心时,发现函数
的对称中心时,发现函数 是一个复合函数,设
是一个复合函数,设 ,
, ,则
,则 ,显然
,显然 有对称中心,设为
有对称中心,设为 ,
, 有反函数
有反函数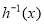 ,则
,则 的对称中心为
的对称中心为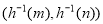 ,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当
,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当 时
时 的对称中心;如果错误,请举出反例,并用正确的方法直接写出当
的对称中心;如果错误,请举出反例,并用正确的方法直接写出当 时
时 的对称中心.
的对称中心. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
 ,
, ,
, 为坐标原点,点
为坐标原点,点 满足
满足 =
= +
+ ,(
,( 为实数);
为实数);(1)当点
 在
在 轴上时,求实数
轴上时,求实数 的值;
的值;(2)四边形
 能否是平行四边形?若是,求实数
能否是平行四边形?若是,求实数 的值;若不是,请说明理由.
的值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
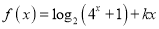 ,(
,(  )是偶函数.
)是偶函数.(1)求
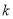 的值;
的值;(2)设函数
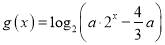 ,其中
,其中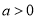 .若函数
.若函数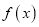 与
与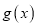 的图象有且只有一个交点,求
的图象有且只有一个交点,求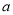 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
, 是定义域为
是定义域为 的奇函数.
的奇函数.(1)确定
 的值;
的值;(2)若
 ,函数
,函数 ,
, ,求
,求 的最小值;
的最小值;(3)若
 ,是否存在正整数
,是否存在正整数 ,使得
,使得 对
对 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
相关试题

