【题目】已知{fn(x)}满足f1(x)= ![]() (x>0),fn+1(x)=f1[fn(x)],
(x>0),fn+1(x)=f1[fn(x)],
(1)求f2(x),f3(x),并猜想fn(x)的表达式;
(2)用数学归纳法证明对fn(x)的猜想.
参考答案:
【答案】
(1)
解: ![]()
![]() 猜想:
猜想: ![]() ,(n∈N*)
,(n∈N*)
(2)
解:下面用数学归纳法证明 ![]() ,(n∈N*)
,(n∈N*)
①当n=1时, ![]() ,显然成立;②假设当n=k(k∈N*)时,猜想成立,即
,显然成立;②假设当n=k(k∈N*)时,猜想成立,即 ![]() ,
,
则当n=k+1时, 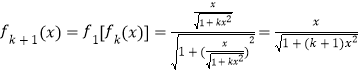
即对n=k+1时,猜想也成立;
结合①②可知,猜想 ![]() 对一切n∈N*都成立
对一切n∈N*都成立
【解析】(1)依题意,计算f2(x)=f1[f1(x)]可求得f2(x),同理可求f3(x);(2)由(1)可猜想 ![]() ,然后用数学归纳法证明即可.
,然后用数学归纳法证明即可.
【考点精析】根据题目的已知条件,利用归纳推理和数学归纳法的定义的相关知识可以得到问题的答案,需要掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理;数学归纳法是证明关于正整数n的命题的一种方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣a(1﹣
 ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( )1008>
)1008>  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
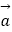 =(sinx,cosx),
=(sinx,cosx), 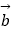 =(sinx,sinx),函数f(x)=
=(sinx,sinx),函数f(x)= 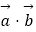 .
.
(1)求f(x)的对称轴方程;
(2)求使f(x)≥1成立的x的取值集合;
(3)若对任意实数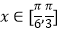 ,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
,不等式f(x)﹣m<2恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
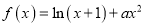 ,
, 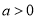 .
.(1)讨论函数
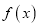 的单调性;
的单调性;(2)若函数
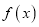 在区间
在区间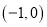 有唯一零点
有唯一零点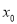 ,证明:
,证明: 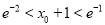 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.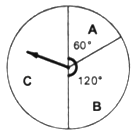
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ=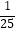 ,方差Dξ=
,方差Dξ= 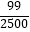 ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.指针位置
A区域
B区域
C区域
返券金额(单位:元)
60
30
0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x2+bx+c在
 上是减函数,在
上是减函数,在 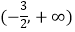 上是增函数,且两个零点x1 , x2满足|x1﹣x2|=2,求二次函数的解析式.
上是增函数,且两个零点x1 , x2满足|x1﹣x2|=2,求二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+
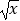 )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
相关试题

