【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),函数f(x)=
=(sinx,sinx),函数f(x)= ![]() .
.
(1)求f(x)的对称轴方程;
(2)求使f(x)≥1成立的x的取值集合;
(3)若对任意实数 ![]() ,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解: ![]()
= ![]()
令 ![]() ,解得
,解得 ![]() .
.
∴f(x)的对称轴方程为 ![]()
(2)解:由f(x)≥1得 ![]() ,即
,即 ![]()
∴ ![]() .
.
故x的取值集合为 ![]() .
.
(3)解:∵ ![]() ,∴
,∴ ![]()
又∵ ![]() 上是增函数,∴
上是增函数,∴ ![]()
又 ![]() ,
,
∴ ![]() 时的最大值是
时的最大值是 ![]()
∵f(x)﹣m<2恒成立,
∴m>f(x)max﹣2,即 ![]()
∴实数m的取值范围是 ![]() .
.
【解析】(1)利用向量的数量积运算、二倍角的公式,两角差的正弦公式化简解析式,由正弦函数的对称轴和整体思想求出f(x)的对称轴方程;(2)由(1)化简f(x)≥1,由正弦函数的图象与性质列出不等式,求出不等式的解集;(3)由由x的范围求出 ![]() 的范围,利用正弦函数的性质求出f(x)的最大值,根据条件和恒成立问题列出不等式,求出实数m的取值范围.
的范围,利用正弦函数的性质求出f(x)的最大值,根据条件和恒成立问题列出不等式,求出实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|3≤x<6},B={y|y=2x , 2≤x<3},U=R.
(1)求A∪B;
(2)求(UA)∩B. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=|x+1|+|x﹣1|.
(1)求f(x)≤x+2的解集;
(2)若不等式f(x)≤log2(a2﹣4a+12)对任意实数a恒成立,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣a(1﹣
 ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( )1008>
)1008>  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
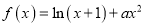 ,
, 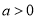 .
.(1)讨论函数
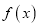 的单调性;
的单调性;(2)若函数
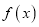 在区间
在区间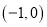 有唯一零点
有唯一零点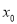 ,证明:
,证明: 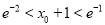 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{fn(x)}满足f1(x)=
 (x>0),fn+1(x)=f1[fn(x)],
(x>0),fn+1(x)=f1[fn(x)],
(1)求f2(x),f3(x),并猜想fn(x)的表达式;
(2)用数学归纳法证明对fn(x)的猜想. -
科目: 来源: 题型:
查看答案和解析>>【题目】五一节期间,某商场为吸引顾客消费推出一项优惠活动,活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见表.
例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.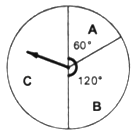
(1)已知顾客甲消费后获得n次转动转盘的机会,已知他每转一次转盘指针落在区域边界的概率为p,每次转动转盘的结果相互独立,设ξ为顾客甲转动转盘指针落在区域边界的次数,ξ的数学期望Eξ=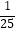 ,方差Dξ=
,方差Dξ= 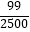 ,求n、p的值;
,求n、p的值;
(2)顾客乙消费280元,并按规则参与了活动,他获得返券的金额记为η(元).求随机变量η的分布列和数学期望.指针位置
A区域
B区域
C区域
返券金额(单位:元)
60
30
0
相关试题

