【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,若直线
轴正半轴为极轴,建立极坐标系,若直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为
为![]() 的倾斜角),曲线
的倾斜角),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() ,
, ![]() ,
, ![]() 与曲线
与曲线![]() 分别交于不同于极点的三点
分别交于不同于极点的三点![]() .
.
(1)求证: ![]() ;
;
(2)当![]() 时,直线
时,直线![]() 过
过![]() 两点,求
两点,求![]() 与
与![]() 的值.
的值.
参考答案:
【答案】(I) 见解析;(II) ![]() ,
, ![]() .
.
【解析】试题分析:(I)利用极坐标方程,可分别求得![]() 值,再利用三角恒等变形可证明所给等式;(2)先利用极坐标方程求出
值,再利用三角恒等变形可证明所给等式;(2)先利用极坐标方程求出![]() 两点的极坐标,再转化为直角坐标系下的坐标,用直线方程的两点式可得直线方程,进一步得
两点的极坐标,再转化为直角坐标系下的坐标,用直线方程的两点式可得直线方程,进一步得![]() 与
与![]() 的值.
的值.
试题解析:(I)证明:依题意, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() .
.
(II) 解:当![]() 时,
时,
![]() 点的极坐标为
点的极坐标为![]() ,
,
![]() 点的极坐标为
点的极坐标为![]() ,
,
化为直角坐标,即![]() ,
, ![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
所以![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取
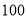 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:分组(岁)
频数

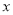

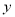
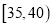
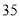
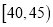
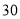
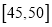
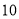
合计
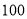
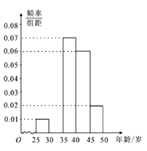
(1)求频率分布表中
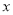 、
、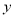 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;(2)在抽取的这
 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取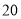 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这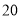 人中随机选取
人中随机选取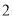 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这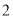 名市民中年龄在
名市民中年龄在 内的人数
内的人数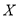 ,求
,求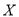 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】 (本小题满分12分)
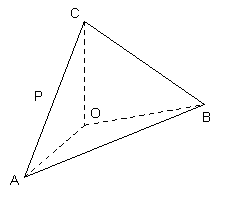
如图, 在四面体ABOC中,
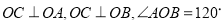 , 且
, 且 .
.
(Ⅰ)设为
 为
为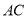 的中点, 证明: 在
的中点, 证明: 在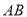 上存在一点
上存在一点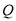 ,使
,使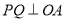 ,并计算
,并计算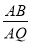 ;
;(Ⅱ)求二面角
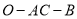 的平面角的余弦值。
的平面角的余弦值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了
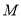 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程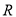 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(1)求
 的值;
的值;(2)若从这
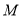 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为
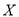 (单位:万元),求
(单位:万元),求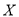 的分布列和数学期望
的分布列和数学期望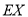 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点
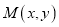 到直线
到直线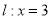 的距离是它到点
的距离是它到点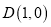 的距离的
的距离的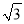 倍.
倍.(1)求动点
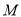 的轨迹
的轨迹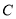 的方程;
的方程;(2)设轨迹
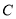 上一动点
上一动点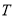 满足:
满足: 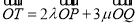 ,其中
,其中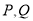 是轨迹
是轨迹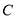 上的点,且直线
上的点,且直线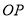 与
与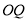 的斜率之积为
的斜率之积为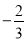 ,若
,若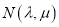 为一动点,
为一动点, 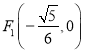 ,
, 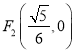 为两定点,求
为两定点,求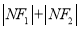 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】求满足下列条件的直线的方程:
(1)经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0;
(2)经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点,且平行于直线4x﹣3y﹣7=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个几何体的三视图如下图,大致画出它的直观图,并求出它的表面积和体积.
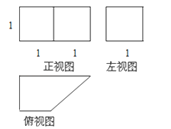
相关试题

