【题目】求满足下列条件的直线的方程:
(1)经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0;
(2)经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点,且平行于直线4x﹣3y﹣7=0.
参考答案:
【答案】解:(1)联立![]() ,解得
,解得![]() ,
,
∴两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点为(﹣2,2),
又直线3x﹣2y+4=0的斜率为![]() ,
,
∴经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0的直线方程为:
y﹣2=-![]() (x+2),即2x+3y﹣2=0;
(x+2),即2x+3y﹣2=0;
(2)联立![]() ,解得
,解得![]() .
.
∴两条直线2x+y﹣8=0和x﹣2y+1=0的交点坐标为(3,2),
又直线4x﹣3y﹣7=0的斜率为![]() ,
,
∴经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点,且平行于直线4x﹣3y﹣7=0的直线方程为:
y﹣2=![]() (x﹣3),即4x﹣3y﹣6=0.
(x﹣3),即4x﹣3y﹣6=0.
【解析】(1)联立两直线方程求得两直线交点,由直线与直线3x﹣2y+4=0垂直求得斜率,代入直线方程的点斜式得答案;
(2)联立两直线方程求得两直线交点,由直线与直线4x﹣3y﹣7=0平行求得斜率,代入直线方程的点斜式得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了
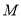 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程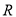 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(1)求
 的值;
的值;(2)若从这
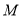 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为
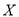 (单位:万元),求
(单位:万元),求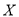 的分布列和数学期望
的分布列和数学期望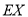 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
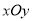 中,以坐标原点
中,以坐标原点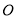 为极点,以
为极点,以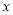 轴正半轴为极轴,建立极坐标系,若直线
轴正半轴为极轴,建立极坐标系,若直线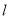 的参数方程为
的参数方程为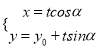 (
(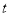 为参数,
为参数, 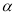 为
为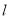 的倾斜角),曲线
的倾斜角),曲线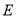 的极坐标方程为
的极坐标方程为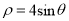 ,射线
,射线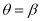 ,
, 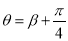 ,
, 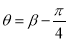 与曲线
与曲线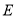 分别交于不同于极点的三点
分别交于不同于极点的三点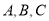 .
.(1)求证:
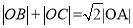 ;
;(2)当
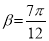 时,直线
时,直线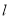 过
过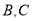 两点,求
两点,求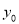 与
与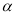 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点
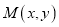 到直线
到直线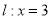 的距离是它到点
的距离是它到点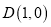 的距离的
的距离的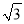 倍.
倍.(1)求动点
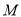 的轨迹
的轨迹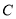 的方程;
的方程;(2)设轨迹
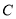 上一动点
上一动点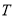 满足:
满足: 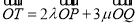 ,其中
,其中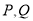 是轨迹
是轨迹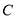 上的点,且直线
上的点,且直线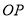 与
与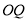 的斜率之积为
的斜率之积为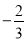 ,若
,若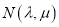 为一动点,
为一动点, 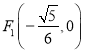 ,
, 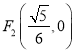 为两定点,求
为两定点,求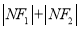 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个几何体的三视图如下图,大致画出它的直观图,并求出它的表面积和体积.
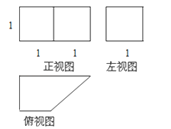
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
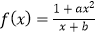 的图象经过点(1,3),并且g(x)=xf(x)是偶函数.
的图象经过点(1,3),并且g(x)=xf(x)是偶函数.
(1)求实数a、b的值;
(2)用定义证明:函数g(x)在区间(1,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
相关试题

