【题目】已知圆心在y轴上的圆C经过点A(1,2)和点B(0,3).
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l在两坐标轴上的截距相等,且被圆C截得的弦长为 ![]() ,求l的方程.
,求l的方程.
参考答案:
【答案】解:(Ⅰ)由已知,得线段AB的中点坐标为( ![]() ,
, ![]() ),
),
直线AB的斜率kAB= ![]() =﹣1,
=﹣1,
所以线段AB的垂直平分线的方程为y﹣ ![]() =x﹣
=x﹣ ![]() ,即x﹣y+2=0.
,即x﹣y+2=0.
由题意,圆C的圆心C在直线x﹣y+2=0上,又在y轴上,所以C(0,2),
半径r=|BC|=1,所以圆C的方程为x2+(y﹣2)2=1. ….(6分)
(Ⅱ)由题意,直线不过原点,设方程为x+y﹣a=0,
∵直线被圆C截得的弦长为 ![]() ,
,
∴圆心到直线的距离为 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a=1或3,
∴所求直线方程为x+y﹣1=0或x+y﹣3=0,
直线过原点,设直线l的方程为y=kx.∴ ![]() =
= ![]() ,
,
∴k= ![]() x,∴所求直线方程为y=
x,∴所求直线方程为y= ![]() x.
x.
综上所述所求直线为x+y﹣1=0或x+y﹣3=0或y= ![]() x
x
【解析】(Ⅰ)求出线段AB的垂直平分线的方程,结合圆C的圆心C在直线x﹣y+2=0上,又在y轴上,求出圆心坐标与半径,即可求圆C的方程;
(Ⅱ)由题意,分类讨论,设方程,利用直线被圆C截得的弦长为 ![]() ,可得圆心到直线的距离为
,可得圆心到直线的距离为 ![]() ,即可求出直线的方程.
,即可求出直线的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,面
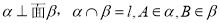 ,点A在直线
,点A在直线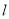 上的射影为
上的射影为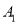 ,点B在直线
,点B在直线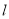 上的射影为
上的射影为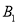 ,连接
,连接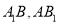 ,已知
,已知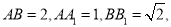 ,
,(Ⅰ)求四面体
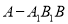 的体积
的体积(Ⅱ)求二面角
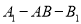 的余弦.
的余弦.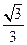
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心和抛物线
的中心和抛物线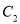 的顶点都在坐标原点
的顶点都在坐标原点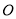 ,
, 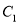 和
和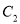 有公共焦点
有公共焦点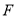 ,点
,点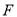 在
在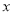 轴正半轴上,且
轴正半轴上,且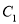 的长轴长、短轴长及点
的长轴长、短轴长及点 到直线
到直线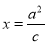 的距离成等比数列。
的距离成等比数列。(Ⅰ)当
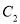 的准线与直线
的准线与直线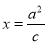 的距离为
的距离为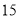 时,求
时,求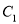 及
及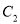 的方程;
的方程;(Ⅱ)设过点
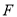 且斜率为
且斜率为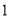 的直线
的直线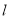 交
交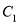 于
于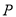 ,
, 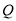 两点,交
两点,交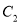 于
于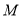 ,
, 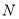 两点。当
两点。当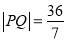 时,求
时,求 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2+log3x,x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.22
C.﹣3
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在研究函数f(x)=
 (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①f(﹣x)+f(x)=0在x∈R时恒成立;
②函数f(x)的值域为(﹣1,1);
③若x1≠x2 , 则一定有f(x1)≠f(x2);
④函数g(x)=f(x)﹣x在R上有三个零点.
其中正确结论的序号有 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
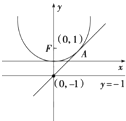
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
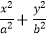 =1(a>b>0)的一个长轴顶点为A(2,0),离心率为
=1(a>b>0)的一个长轴顶点为A(2,0),离心率为 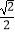 ,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△AMN的面积为 时,求k的值.
时,求k的值.
相关试题

