【题目】(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
优 秀 | 不优秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
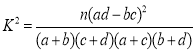
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】在犯错误的概率不超过0.01的前提下不能认为成绩与班级有关系。
【解析】本试题主要是考查了独立性检验的思想的运用,求解分类变量的相关性问题的判定。只要将已知的数据代入到关系式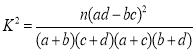 中计算并比较列表中的数据可得结论。
中计算并比较列表中的数据可得结论。
![]()
因为![]()
所以在犯错误的概率不超过0.01的前提下不能认为成绩与班级有关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数,例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:
①函数f(x)=x2(x∈R)是单函数;
②函数f(x)=
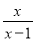 是单函数;
是单函数;③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是________.(写出所有真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线C的参数方程为
中,曲线C的参数方程为 (其中
(其中 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系中,直线
轴的正半轴为极轴建立极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求C的普通方程和直线
 的倾斜角;
的倾斜角;(Ⅱ)设点
 (0,2),
(0,2), 和
和 交于
交于 两点,求
两点,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
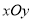 中,曲线
中,曲线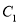 过点
过点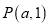 ,其参数方程为
,其参数方程为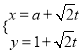 (
(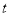 为参数,
为参数, 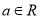 ),以
),以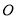 为极点,
为极点, 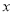 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线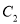 的极坐标方程为
的极坐标方程为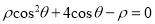 .
.(1)求曲线
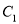 的普通方程和曲线
的普通方程和曲线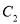 的直角坐标方程;
的直角坐标方程;(2)已知曲线
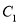 与曲线
与曲线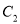 交于
交于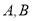 两点,且
两点,且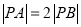 ,求实数
,求实数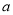 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1=4,D是A1C1中点.
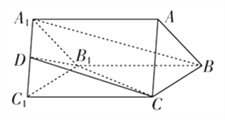
(1)求证:A1B∥平面B1CD;
(2)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设
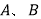 为两个同高的几何体,
为两个同高的几何体,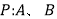 的体积不相等,
的体积不相等,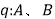 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,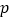 是
是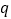 的( )
的( )A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=
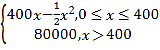 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
相关试题

