【题目】已知a,b,c分别为△ABC中角A,B,C的对边,函数 ![]() 且f(A)=5.
且f(A)=5.
(1)求角A的大小;
(2)若a=2,求△ABC面积的最大值.
参考答案:
【答案】
(1)解:由题意可得: ![]()
=3+ ![]() sin2A+cos2A+1=4+2sin(2A+
sin2A+cos2A+1=4+2sin(2A+ ![]() ),
),
∴sin(2A+ ![]() )=
)= ![]() ,∵A∈(0,π),
,∵A∈(0,π),
∴2A+ ![]() ∈(
∈( ![]() ,
, ![]() ),∴2A+
),∴2A+ ![]() =
= ![]() ,∴A=
,∴A= ![]()
(2)解:由余弦定理可得: ![]() ,
,
即4=b2+c2﹣bc≥bc(当且仅当b=c=2时“=”成立),即bc≤4,
∴ ![]() ,
,
故△ABC面积的最大值是 ![]()
【解析】(1)利用三角恒等变换求得f(A)的解析式,由f(A)=5求得 sin(2A+ ![]() ) 的值,从而求得2A+
) 的值,从而求得2A+ ![]() 的值,可得A的值.(2)利用余弦定理,基本不等式,求得bc的最大值,可得△ABC面积
的值,可得A的值.(2)利用余弦定理,基本不等式,求得bc的最大值,可得△ABC面积 ![]() bcsinA的最大值.
bcsinA的最大值.
【考点精析】利用余弦定理的定义对题目进行判断即可得到答案,需要熟知余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
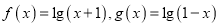 ,
, 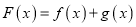 .
.(1)求函数
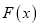 的定义域;
的定义域;(2)判断函数
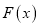 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)判断函数
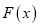 在区间
在区间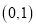 上的单调性,并加以证明.
上的单调性,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面ADE. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
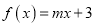 ,
, 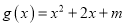 .
.(1)判断函数
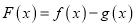 是否有零点;
是否有零点;(2)设函数
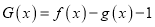 ,若
,若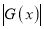 在
在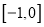 上是减函数,求实数
上是减函数,求实数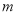 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣x+1与椭圆
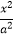 +
+ 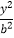 =1(a>b>0)相交于A、B两点.
=1(a>b>0)相交于A、B两点.
①若椭圆的离心率为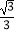 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
②若向量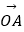 与向量
与向量 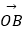 互相垂直(其中O为坐标原点),当椭圆的离心率e∈[
互相垂直(其中O为坐标原点),当椭圆的离心率e∈[  ,
, 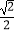 ]时,求椭圆的长轴长的最大值.
]时,求椭圆的长轴长的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若
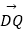 =t
=t 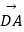 .
. 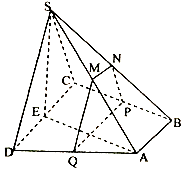
(1)当t= 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为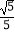 ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,证明:e﹣2<a<1.
相关试题

