【题目】设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=![]() 的a的值,并求此时函数的最大值.
的a的值,并求此时函数的最大值.
参考答案:
【答案】见解析
【解析】解 令cosx=t,t∈[-1,1],
则y=2t2-2at-(2a+1)
=2(t-![]() )2-
)2-![]() -2a-1,
-2a-1,
关于t的二次函数的对称轴是t=![]() ,
,
当![]() <-1,即a<-2时,
<-1,即a<-2时,
函数y在t∈[-1,1]上是单调递增,
所以f(a)=f(-1)=1≠![]() ;
;
当![]() >1,即a>2时,
>1,即a>2时,
函数y在t∈[-1,1]上是单调递减,
所以f(a)=f(1)=-4a+1=![]() ,
,
解得a=![]() ,这与a>2矛盾;
,这与a>2矛盾;
当-1≤![]() ≤1,即-2≤a≤2时,
≤1,即-2≤a≤2时,
f(a)=-![]() -2a-1=
-2a-1=![]() ,
,
即a2+4a+3=0,解得a=-1或a=-3,
因为-2≤a≤2,所以a=-1.
所以y=2t2+2t+1,t∈[-1,1],所以当t=1时,
函数取得最大值ymax=2+2+1=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
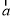 =(sinx,cosx),
=(sinx,cosx),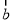 =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|< ).函数
).函数f(x)=
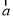
 且f(
且f(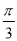 -x)=f(x).
-x)=f(x).(Ⅰ)求f(x)的解析式及单调递增区间;
(Ⅱ)将f(x)的图象向右平移
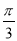 单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,
单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,  ]上恒成立,求实数a的取值范围.
]上恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出四个命题
(1)若sin2A=sin2B,则△ABC为等腰三角形;
(2)若sinA=cosB,则△ABC为直角三角形;
(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;
(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.
以上正确命题的是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
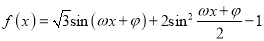 (
(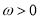 ,
, 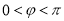 )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为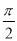 .
.(1)当
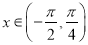 时,求
时,求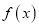 的单调递减区间;
的单调递减区间;(2)将函数
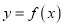 的图象沿
的图象沿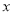 轴方向向右平移
轴方向向右平移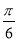 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的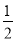 (纵坐标不变),得到函数
(纵坐标不变),得到函数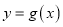 的图象.当
的图象.当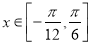 时,求函数
时,求函数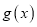 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA-csinC=b(sinA-sinB).
(Ⅰ)求角C的大小;
(Ⅱ)若边长c=4,求△ABC的周长最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(3),f(-
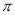 )的大小顺序是:( )
)的大小顺序是:( )A. f(-
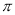 )>f(3)>f(-2) B. f(-
)>f(3)>f(-2) B. f(-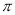 ) >f(-2)>f(3)
) >f(-2)>f(3)C. f(-2)>f(3)> f(-
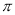 ) D. f(3)>f(-2)> f(-
) D. f(3)>f(-2)> f(-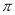 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】本着健康、低碳的生活理念,租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费,超过两小时的部分每小时2元(不足1小时的部分按1小时计算).甲乙两人相互独立租车(各租一车一次).设甲、乙不超过两小时还车的概率分别为
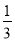 ,
,  ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为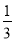 ,
,  ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.(1)求出甲、乙所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
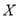 ,求随机变量
,求随机变量 的概率分布和期望.
的概率分布和期望.
相关试题

