搜索
【题目】给出四个命题
（1）若sin2A=sin2B，则△ABC为等腰三角形；
（2）若sinA=cosB，则△ABC为直角三角形；
（3）若sin2A+sin2B+sin2C＜2，则△ABC为钝角三角形；
（4）若cos（A－B）cos（B－C）cos（C－A）=1，则△ABC为正三角形．
以上正确命题的是_______．
参考答案：
【答案】（3）（4）
【解析】
试题分析：（1）中满足
或
，所以三角形为等腰三角形或直角三角形；（2）中
，但三角形不是直角三角形；（3）中由正弦定理
；（4）若cos（A-B）cos（B-C）cos（C-A）=1由三角函数的有界性可知三个都是1或者两个-1一个1都是1显然成立，如果两个-1又不可能，所以命题是三角形为正三角形的充要条件，所以（4）正确
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)＝x3－3ax－1，a≠0.
(1)求f(x)的单调区间；
(2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图象有三个不同的交点，求m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x3-3ax+e，g（x）=1-lnx，其中e为自然对数的底数.
（I）若曲线y=f（x）在点（1，f（1））处的切线与直线l：x+2y=0垂直，求实数a的值；
（II）设函数F（x）=-x[g（x）+
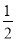x-2]，若F（x）在区间（m,m+1）（m∈Z）内存在唯一的极值点，求m的值；（III）用max{m，n}表示m，n中的较大者，记函数h（x）=max{f（x），g（x）}（x>0）. 若函数h（x）在（0，+∞）上恰有2个零点，求实数a的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
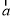=（sinx，cosx），
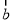=（cosφ，sinφ）（|φ|＜
）．函数f（x）=
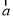
且f（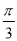
－x）=f（x）．（Ⅰ）求f（x）的解析式及单调递增区间；
（Ⅱ）将f（x）的图象向右平移
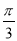单位得g（x）的图象，若g（x）+1≤ax+cosx在x∈[0， 
]上恒成立，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
（
， 
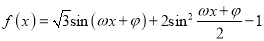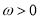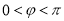）为奇函数，且相邻两对称轴间的距离为
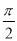.（1）当
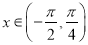时，求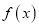
的单调递减区间；（2）将函数
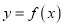的图象沿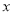
轴方向向右平移
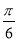个单位长度，再把横坐标缩短到原来的
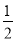（纵坐标不变），得到函数
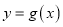的图象.当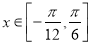
时，求函数
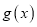的值域. -
科目： 来源： 题型：
查看答案和解析>>【题目】设关于x的函数y＝2cos2x－2acosx－(2a＋1)的最小值为f(a)，试确定满足f(a)＝
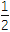的a的值，并求此时函数的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，内角A，B，C所对的边分别为a，b，c，且满足asinA-csinC=b(sinA－sinB）．
（Ⅰ）求角C的大小；
（Ⅱ）若边长c=4，求△ABC的周长最大值．
相关试题
