【题目】已知函数f(x)=![]() (c为常数),且f(1)=0.
(c为常数),且f(1)=0.
(1)求c的值;
(2)证明函数f(x)在[0,2]上是单调递增函数;
(3)已知函数g(x)=f(ex),判断函数g(x)的奇偶性.
参考答案:
【答案】(1)1;(2)见解析;(3)g(x)为奇函数.
【解析】
试题(1)根据f(1)=![]() =0,解得c=1;
=0,解得c=1;
(2)运用单调性定义证明;
(3)运用奇偶性定义证明.
解:(1)因为f(1)=![]() =0,所以c=1,即c的值为1;
=0,所以c=1,即c的值为1;
(2)f(x)=![]() =1﹣
=1﹣![]() ,在[0,2]单调递增,证明如下:
,在[0,2]单调递增,证明如下:
任取x1,x2∈[0,2],且x1<x2,
则f(x1)﹣f(x2)=(1﹣![]() )﹣(1﹣
)﹣(1﹣![]() )
)
=2[![]() ﹣
﹣![]() ]=2
]=2![]() <0,
<0,
即f(x1)<f(x2),
所以,f(x)在[0,2]单调递增;
(3)g(x)=f(ex)=![]() ,定义域为R,
,定义域为R,
g(﹣x)=![]() =
=![]() =﹣
=﹣![]() =﹣g(x),
=﹣g(x),
所以,g(x)为奇函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设
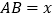 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.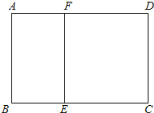
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于茎叶图的说法,结论错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是25
C. 乙的众数是21 D. 甲的平均数比乙的大
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是 ( )
A. 某事件发生的概率为1.1 B. 对立事件也是互斥事件
C. 不能同时发生的的两个事件是两个对立事件 D. 某事件发生的概率是随着实验次数的变化而变化的
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知指数函数
 满足
满足 ,定义域为
,定义域为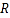 的函数
的函数 是奇函数.
是奇函数.(1)求函数
 的解析式;
的解析式;(2)若函数
 在
在 上有零点,求
上有零点,求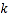 的取值范围;
的取值范围;(3)若对任意的
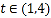 ,不等式
,不等式 恒成立,求实数
恒成立,求实数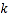 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为1的正方体
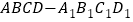 中,点
中,点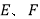 分别是棱
分别是棱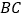 ,
,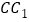 的中点,
的中点,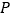 是侧面
是侧面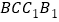 内一点,若
内一点,若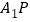
 平面
平面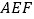 ,则线段
,则线段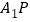 长度的取值范围是( )
长度的取值范围是( )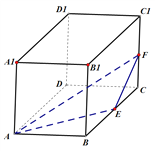
A.
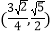 B.
B. 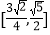 C.
C. 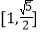 D.
D. 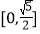
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
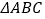 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 成等差数列
成等差数列(1)若
 ,求
,求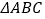 的面积
的面积(2)若
 成等比数列,试判断
成等比数列,试判断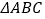 的形状
的形状
相关试题

