【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 为定义在
为定义在![]() 上的“局部奇函数”;
上的“局部奇函数”;
![]() 曲线
曲线![]() 与
与![]() 轴交于不同的两点;
轴交于不同的两点;
若![]() 为假命题,
为假命题, ![]() 为真命题,求
为真命题,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】![]() 或
或![]() 或
或![]()
【解析】试题分析:首先根据已知条件并结合换元法和二次函数在区间上的最值以及一元二次方程根的情况分别求出命题![]() ,
, ![]() 为真命题时所满足的
为真命题时所满足的![]() 的取值范围,然后根据已知条件可知命题
的取值范围,然后根据已知条件可知命题![]() ,
, ![]() 中一个为真命题,一个为假命题,并利用补集的思想求出
中一个为真命题,一个为假命题,并利用补集的思想求出![]() 的取值范围.
的取值范围.
试题解析:若p为真,则由于![]() 为
为![]() 的局部奇函数,从而
的局部奇函数,从而![]() ,即
,即![]() 在
在![]() 上有解,令
上有解,令![]() ,则
,则![]() ,又
,又![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,从而
上递增,从而![]() ,得
,得![]() ,故有
,故有![]() . 若
. 若![]() 为真,则有
为真,则有![]() ,得
,得![]() 或
或![]() . 又由“
. 又由“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,则
”为真命题,则![]() 与
与![]() 一真一假;若
一真一假;若![]() 真
真![]() 假,则
假,则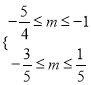 ,得无交集;若
,得无交集;若![]() 假
假![]() 真,则
真,则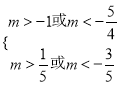 ,得
,得![]() 或
或![]() 或
或![]() ,综上知
,综上知![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的 处有一外国船只,且
处有一外国船只,且 岛位于海监船正东
岛位于海监船正东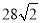 海里处.
海里处.
(1)求此时该外国船只与
 岛的距离;
岛的距离;(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离
 岛24海里处,不让其进入
岛24海里处,不让其进入 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据: 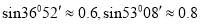 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个
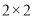 的列联表;
的列联表;(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
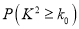
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
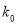
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:
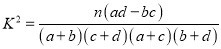 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前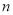 项和为
项和为 ,且满足
,且满足 .
.(1)求证:数列
 为等比数列;
为等比数列;(2)若
 ,求
,求 的前
的前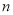 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我海监船在
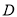 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至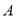 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的 处有一外国船只,且
处有一外国船只,且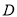 岛位于海监船正东
岛位于海监船正东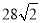 海里处.
海里处.
(1)求此时该外国船只与
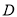 岛的距离;
岛的距离;(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离
 岛24海里处,不让其进入
岛24海里处,不让其进入 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据: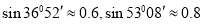 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型
特大套
大套
经济适用房
舒适
100
150

标准
300
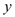
600
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求
 ,
,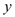 的值;
的值;(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
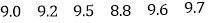
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为
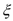 ,求
,求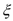 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
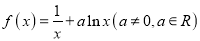 .
.(1)若
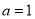 ,求函数
,求函数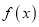 的极值和单调区间;
的极值和单调区间;(2)若在区间
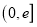 上至少存在一点
上至少存在一点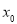 ,使得
,使得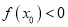 成立,求实数
成立,求实数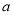 的取值范围.
的取值范围.
相关试题

