【题目】为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天的PM2.5日平均浓度(单位:微克/立方米)是监测数据,得到甲地PM2.5日平均浓度的频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
甲地20天PM2.5日平均浓度频率分布直方图

乙地20天PM2.5日平均浓度频数分布表

(1)根据乙地20天PM2.5日平均浓度的频数分布表作出相应的频率分布直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度;(不要求计算出具体值,给出结论即可)
(2)求甲地20天PM2.5日平均浓度的中位数;
(3)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:

记事件![]() :“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件
:“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件![]() 的概率.
的概率.
参考答案:
【答案】(1)答案见解析;(2)![]() 微克/立方米;(3)0.9.
微克/立方米;(3)0.9.
【解析】分析:(1)做出乙地20天PM2.5日平均浓度的频率分布直方图;由图判断平均值和数据分散程度。
(2)根据频率分布直方图中位数求法,求得频率为0.5时对应的PM2.5值即可。
(3)先求出甲地市民对空气质量的满意度等级为不满意的概率,再利用对立事件的概率求事件![]() 的概率。
的概率。
详解:(1)乙地20天PM2.5日平均浓度的频率分布直方图如图所示:
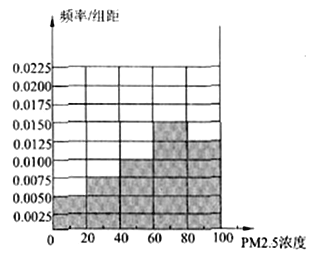
由此可知,甲地PM2.5日平均浓度的平均值低于乙地PM2.5日平均浓度的平均值;而且甲地的数据比较集中,乙地的数据比较分散.
(2)∵甲地PM2.5日平均浓度在![]() 之间的频率为
之间的频率为![]()
在![]() 之间的频率为
之间的频率为![]() ;
;
∴![]() ,
,
∴中位数一定在区间![]() 之间,设为
之间,设为![]() ,则
,则![]() ,
,
解得![]()
∴甲地PM2.5日平均浓度的中位数为![]() 微克/立方米.
微克/立方米.
(3)因为当PM2.5日平均浓度超过60微克/立方米时,市民对空气质量不满意,
所以![]()
又由对立事件计算公式,得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A、B、C所对的边长分别为a、b、c,且acos B=3,bsin A=4.
(1)求边长a;
(2)若△ABC的面积S=10,求△ABC的周长l.
-
科目: 来源: 题型:
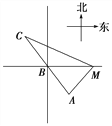
查看答案和解析>>【题目】如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于1 km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是直角梯形,
是直角梯形, ,
, ,
, ,
, ,又
,又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)(文科)求三棱锥
 的体积.
的体积.(理科)求二面角
 平面角正切值的大小.
平面角正切值的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=6,cos B=
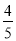 ,C=
,C=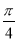 .
.(1)求AB的长;
(2)求cos
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
 中,底面
中,底面 是
是 的菱形,侧面
的菱形,侧面 为正三角形,其所在平面垂直于底面
为正三角形,其所在平面垂直于底面 .
.
(1)若
 为线段
为线段 的中点,求证:
的中点,求证: 平面
平面 ;
;(2)若
 为边
为边 的中点,能否在棱
的中点,能否在棱 上找到一点
上找到一点 ,使平面
,使平面 平面
平面 ?并证明你的结论.
?并证明你的结论.
相关试题

