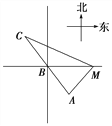
【题目】如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于1 km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
参考答案:
【答案】![]()
【解析】试题分析:由S△MAB与S△MBC底相同高相同得S△MAB=S△MBC;利用三角形面积公式代入整理得MC=![]() MA,然后根据余弦定理得AC2=MA2+MC2-2MA·MC·cos 75°=
MA,然后根据余弦定理得AC2=MA2+MC2-2MA·MC·cos 75°=![]() MA;最后根据三角形的面积公式得
MA;最后根据三角形的面积公式得![]() MA·MC·sin 75°=
MA·MC·sin 75°=![]() AC·h,整理求出h=
AC·h,整理求出h=![]() (km).
(km).
试题解析:
由题意∠CMB=30°,∠AMB=45°,
因为AB=BC=1,所以S△MAB=S△MBC,
即![]() MA·MB·sin 45°=
MA·MB·sin 45°=![]() MC·MB·sin 30°,
MC·MB·sin 30°,
所以MC=![]() MA,
MA,
在△MAC中,由余弦定理AC2=MA2+MC2-2MA·MC·cos 75°,
所以MA2=![]() ,
,
设M到AB的距离为h,则由△MAC的面积得
![]() MA·MC·sin 75°=
MA·MC·sin 75°=![]() AC·h,
AC·h,
所以h=![]() ·sin 75°=
·sin 75°=![]() ·
·![]() ·sin 75°=
·sin 75°=![]() (km).
(km).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B=

(1)求边c的长;
(2)求角B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A、B、C所对的边长分别为a、b、c,且acos B=3,bsin A=4.
(1)求边长a;
(2)若△ABC的面积S=10,求△ABC的周长l.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天的PM2.5日平均浓度(单位:微克/立方米)是监测数据,得到甲地PM2.5日平均浓度的频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
甲地20天PM2.5日平均浓度频率分布直方图

乙地20天PM2.5日平均浓度频数分布表

(1)根据乙地20天PM2.5日平均浓度的频数分布表作出相应的频率分布直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度;(不要求计算出具体值,给出结论即可)
(2)求甲地20天PM2.5日平均浓度的中位数;
(3)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:

记事件
 :“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件
:“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是直角梯形,
是直角梯形, ,
, ,
, ,
, ,又
,又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)(文科)求三棱锥
 的体积.
的体积.(理科)求二面角
 平面角正切值的大小.
平面角正切值的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AC=6,cos B=
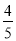 ,C=
,C=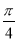 .
.(1)求AB的长;
(2)求cos
 的值.
的值.
相关试题

