【题目】无穷数列![]() 满足:
满足:![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
,![]() 为前
为前![]() 项
项![]() 、
、![]() 、
、![]() 、
、![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知命题![]() 存在正整数
存在正整数![]() ,使得
,使得![]() ,判断命题
,判断命题![]() 的真假并说明理由;
的真假并说明理由;
(3)若对任意正整数![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)真命题,证明见解析;(3)
;(2)真命题,证明见解析;(3)![]() .
.
【解析】
(1)根据题意直接写出![]() 、
、![]() 、
、![]() 的值,可得出结果;
的值,可得出结果;
(2)分![]() 和
和![]() 两种情况讨论,找出使得等式
两种情况讨论,找出使得等式![]() 成立的正整数
成立的正整数![]() ,可得知命题
,可得知命题![]() 为真命题;
为真命题;
(3)先证明出“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”的充要条件,由此可得出
成立”的充要条件,由此可得出![]() ,然后利用定义得出
,然后利用定义得出![]() ,由此可得出
,由此可得出![]() 的值.
的值.
(1)根据题意知,对任意正整数![]() ,
,![]() 为前
为前![]() 项
项![]() 、
、![]() 、
、![]() 、
、![]() 中等于
中等于![]() 的项的个数,
的项的个数,
因此,![]() ,
,![]() ,
,![]() ;
;
(2)真命题,证明如下:
①当![]() 时,则
时,则![]() ,
,![]() ,
,![]() ,此时,当
,此时,当![]() 时,
时,![]() ;
;
②当![]() 时,设
时,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
此时,当![]() 时,
时,![]() .
.
综上所述,命题![]() 为真命题;
为真命题;
(3)先证明:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”的充要条件.
成立”的充要条件.
假设存在![]() ,使得“存在
,使得“存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立”.
成立”.
则数列![]() 的前
的前![]() 项为
项为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
后面的项顺次为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故对任意的![]() ,
,![]()
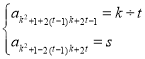 ,
,
对任意的![]() ,取
,取![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数,则
的最大整数,则![]() ,
,
令![]() ,则
,则![]() ,此时
,此时![]() ,
,![]()
有![]() ,这与
,这与![]() 矛盾,
矛盾,
故若存在![]() ,当
,当![]() 时,恒有
时,恒有![]() 成立,必有
成立,必有![]() ;从而得证.
;从而得证.
另外:当![]() 时,数列
时,数列![]() 为
为![]() ,
,
故![]() ,则
,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面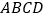 为直角梯形,
为直角梯形,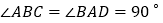 ,
,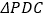 和
和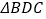 均为等边三角形,且平面
均为等边三角形,且平面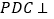 平面
平面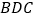 ,点
,点 为
为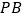 中点.
中点.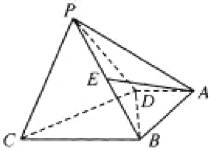
(Ⅰ)求证:
 平面
平面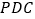 ;
;(Ⅱ)若
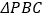 的面积为
的面积为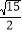 ,求三棱锥
,求三棱锥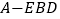 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“我将来要当一名麦田里的守望者,有那么一群孩子在一块麦田里玩,几千万的小孩子,附近没有一个大人,我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形
 的麦田里成为守望者,如图所示,为了分割麦田,他将
的麦田里成为守望者,如图所示,为了分割麦田,他将 连接,设
连接,设 中边
中边 所对的角为
所对的角为 ,
, 中边
中边 所对的角为
所对的角为 ,经测量已知
,经测量已知 ,
, .
.
(1)霍尔顿发现无论
 多长,
多长, 为一个定值,请你验证霍尔顿的结论,并求出这个定值;
为一个定值,请你验证霍尔顿的结论,并求出这个定值;(2)霍尔顿发现麦田的生长于土地面积的平方呈正相关,记
 与
与 的面积分别为
的面积分别为 和
和 ,为了更好地规划麦田,请你帮助霍尔顿求出
,为了更好地规划麦田,请你帮助霍尔顿求出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在直角坐标系
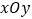 中,点
中,点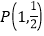 到抛物线
到抛物线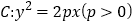 的准线的距离为
的准线的距离为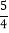 .点
.点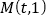 是
是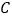 上的定点,
上的定点,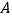 ,
,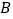 是
是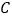 上的两动点,且线段
上的两动点,且线段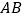 的中点
的中点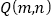 在直线
在直线 上.
上.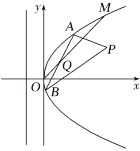
(Ⅰ)求曲线
 的方程及
的方程及 的值;
的值;(Ⅱ)记
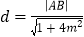 ,求
,求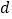 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I)若曲线
 上点
上点 处的切线过点
处的切线过点 ,求函数
,求函数 的单调减区间;
的单调减区间;(II)若函数
 在区间
在区间 内无零点,求实数
内无零点,求实数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
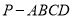 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,  ,
, 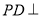 底面
底面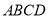 .
.(1)证明:
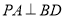 ;
;(2)设
 ,求点
,求点 到面
到面 的距离.
的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面几种推理过程是演绎推理的是( )
A. 在数列|
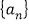 中,
中,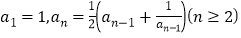 由此归纳出
由此归纳出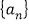 的通项公式
的通项公式B. 由平面三角形的性质,推测空间四面体性质
C. 某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人
D. 两条直线平行,同旁内角互补,如果
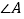 和
和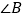 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则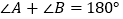
相关试题

