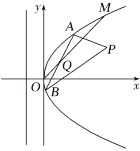
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由抛物线准线方程及P到准线的距离,可求得![]() ,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
(Ⅱ)求直线OM方程,点Q在直线OM上,根据直线方程表示点Q坐标,消去参数n,
利用点差法表示出直线AB斜率,进而求出直线方程,将直线AB方程与抛物线方程联立,用弦长公式求弦长,从而将d表示为关于m的函数,根据m范围求最值.
详解:(1)![]() 的准线为
的准线为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .又点
.又点![]() 在曲线
在曲线![]() 上,∴
上,∴![]() .
.
(2)由(1)知,点![]() ,从而
,从而![]() ,即点
,即点![]() ,
,
依题意,直线![]() 的斜率存在,且不为
的斜率存在,且不为![]() ,
,
设直线![]() 的斜率为
的斜率为![]() .且
.且![]() ,
,![]() ,
,
由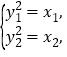 得
得![]() ,故
,故![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
从而![]() .
.
∴![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立,
时,上式等号成立,
又![]() 满足
满足![]() .∴
.∴![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-
市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-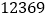 ”的绿色环保活动小组对
”的绿色环保活动小组对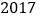 年
年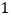 月-
月-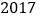 年
年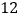 月(一月)内空气质量指数
月(一月)内空气质量指数 进行监测,如表是在这一年随机抽取的
进行监测,如表是在这一年随机抽取的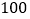 天的统计结果:
天的统计结果:指数

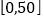
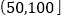
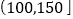
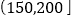
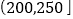
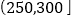
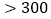
空气质量
优
良
轻微污染
轻微污染
中度污染
中重度污染
重度污染
天数
4
13
18
30
9
11
15
(Ⅰ)若
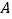 市某企业每天由空气污染造成的经济损失
市某企业每天由空气污染造成的经济损失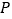 (单位:元)与空气质量指数
(单位:元)与空气质量指数 (记为
(记为 )的关系为:
)的关系为: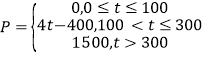 ,,在这一年内随机抽取一天,估计该天经济损失
,,在这一年内随机抽取一天,估计该天经济损失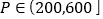 元的概率;
元的概率;(Ⅱ)若本次抽取的样本数据有
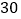 天是在供暖季节,其中有
天是在供暖季节,其中有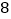 天为重度污染,完成
天为重度污染,完成 列联表,并判断是否有
列联表,并判断是否有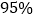 的把握认为
的把握认为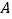 市本年度空气重度污染与供暖有关?
市本年度空气重度污染与供暖有关?
下面临界值表供参考.
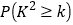
0.15
0.10
0.05
0.010
0.005
0.001

2.072
2.706
3.841
6.635
7.879
10.828
参考公式:
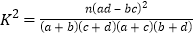 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面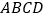 为直角梯形,
为直角梯形,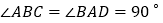 ,
,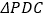 和
和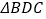 均为等边三角形,且平面
均为等边三角形,且平面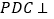 平面
平面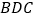 ,点
,点 为
为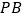 中点.
中点.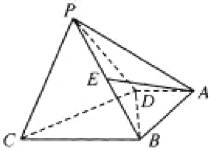
(Ⅰ)求证:
 平面
平面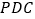 ;
;(Ⅱ)若
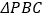 的面积为
的面积为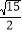 ,求三棱锥
,求三棱锥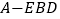 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“我将来要当一名麦田里的守望者,有那么一群孩子在一块麦田里玩,几千万的小孩子,附近没有一个大人,我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形
 的麦田里成为守望者,如图所示,为了分割麦田,他将
的麦田里成为守望者,如图所示,为了分割麦田,他将 连接,设
连接,设 中边
中边 所对的角为
所对的角为 ,
, 中边
中边 所对的角为
所对的角为 ,经测量已知
,经测量已知 ,
, .
.
(1)霍尔顿发现无论
 多长,
多长, 为一个定值,请你验证霍尔顿的结论,并求出这个定值;
为一个定值,请你验证霍尔顿的结论,并求出这个定值;(2)霍尔顿发现麦田的生长于土地面积的平方呈正相关,记
 与
与 的面积分别为
的面积分别为 和
和 ,为了更好地规划麦田,请你帮助霍尔顿求出
,为了更好地规划麦田,请你帮助霍尔顿求出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】无穷数列
 满足:
满足: 为正整数,且对任意正整数
为正整数,且对任意正整数 ,
,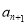 为前
为前 项
项 、
、 、
、 、
、 中等于
中等于 的项的个数.
的项的个数.(1)若
 ,求
,求 和
和 的值;
的值;(2)已知命题
 存在正整数
存在正整数 ,使得
,使得 ,判断命题
,判断命题 的真假并说明理由;
的真假并说明理由;(3)若对任意正整数
 ,都有
,都有 恒成立,求
恒成立,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I)若曲线
 上点
上点 处的切线过点
处的切线过点 ,求函数
,求函数 的单调减区间;
的单调减区间;(II)若函数
 在区间
在区间 内无零点,求实数
内无零点,求实数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
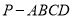 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,  ,
, 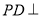 底面
底面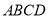 .
.(1)证明:
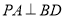 ;
;(2)设
 ,求点
,求点 到面
到面 的距离.
的距离.
相关试题

